
【题目】已知二次函数![]() (
(![]() 、
、![]() 为常数且
为常数且![]() ),满足条件
),满足条件![]() ,且方程
,且方程![]() 有等根.
有等根.
(1)若![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,
,![]() ,使
,使![]() 当定义域为
当定义域为![]() 时,值域为
时,值域为![]() ?如果存在,求出
?如果存在,求出![]() ,
,![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】(1)![]() (2)存在
(2)存在![]() ,
,![]() 满足题意,详见解析
满足题意,详见解析
【解析】
(1)由已知中![]() ,可得
,可得![]() 的图象关于直线
的图象关于直线![]() 对称,结合方程
对称,结合方程![]() 有等根其
有等根其![]() ,我们可构造关于
,我们可构造关于![]() 的方程组,解方程组求出
的方程组,解方程组求出![]() 的值,即可得到
的值,即可得到![]() 的解析式,然后针对
的解析式,然后针对![]() ,
,![]() 恒成立,转化为函数
恒成立,转化为函数![]() 在
在![]() 上恒成立,求其最小值,列不等式求出实数
上恒成立,求其最小值,列不等式求出实数![]() 的取值范围;
的取值范围;
(2)由(1)中函数的解析式,我们根据![]() 的定义域和值域分别为
的定义域和值域分别为![]() 和
和![]() ,我们易判断出函数在
,我们易判断出函数在![]() 的单调性,进而构造出满足条件的方程,解方程即可得到答案.
的单调性,进而构造出满足条件的方程,解方程即可得到答案.
解:(1)![]() 满足
满足![]() ,
,
![]() 的图像关于直线
的图像关于直线![]() 对称,
对称,
![]() ,①
,①
又方程![]() 有等根,即
有等根,即![]() 有等根,
有等根,
![]() ,②
,②
由①②得![]() ,
,
![]() ,
,
令![]() ,
,
则![]() 在
在![]() 上恒成立,
上恒成立,
所以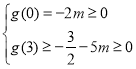 ,
,
解得![]() ;
;
(2)由(1)可得![]() ,
,
假设存在![]() 、
、![]() ,使
,使![]() 当定义域为
当定义域为![]() 时,值域为
时,值域为![]() ,
,
则必有![]() ,即
,即![]() ,即
,即![]() 必在对称轴的左侧,且
必在对称轴的左侧,且![]() 在
在![]() 单调递增,
单调递增,
所以,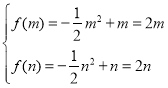 又由
又由![]() ,
,
解得![]() ,
,
所以存在![]() ,
,![]() 满足题意.
满足题意.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解学生对食堂伙食的满意程度,组织学生给食堂打分(分数为整数,满分100分),从中随机抽取一个容量为![]() 的样本,发现所有数据均在
的样本,发现所有数据均在![]() 内.现将这些分数分成以下
内.现将这些分数分成以下![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并画出了样本的频率分布直方图,部分图形如图所示.观察图形,回答下列问题:
,并画出了样本的频率分布直方图,部分图形如图所示.观察图形,回答下列问题:
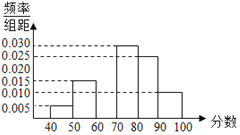
(1)算出第三组![]() 的频数,并补全频率分布直方图;
的频数,并补全频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数和平均数,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2014年到2018年人口总数![]() (单位:十万)与年份(用
(单位:十万)与年份(用![]() 表示)的关系如表所示:
表示)的关系如表所示:
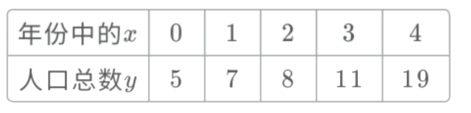
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(3)据此估计2019年该城市人口总数.
(参考数据: ![]()
![]() )
)
参考公式:线性回归方程为![]() ,其中
,其中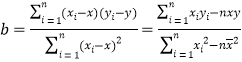 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量![]() (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量![]() (百斤)与使用某种液体肥料
(百斤)与使用某种液体肥料![]() (千克)之间对应数据为如图所示的折线图.
(千克)之间对应数据为如图所示的折线图.

(1)依据数据的折线图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01);(若
并加以说明(精确到0.01);(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如表关系:
限制,并有如表关系:

若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.以过去50周的周光照量的频率作为周光照量发生的概率,商家欲使周总利润的均值达到最大,应安装光照控制仪多少台?
附:相关系数公式 ,参考数据
,参考数据![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:如果对任意的x1,x2∈R,都有f(![]() )
)![]() ,则称函数f(x)是R上的凹函数,已知二次函数f(x)=ax2+x(a∈R,a≠0)
,则称函数f(x)是R上的凹函数,已知二次函数f(x)=ax2+x(a∈R,a≠0)
(1)当a=1,x∈[﹣2,2]时,求函数f(x)的值域;
(2)当a=1时,试判断函数f(x)是否为凹函数,并说明理由;
(3)如果函数f(x)对任意的x∈[0,1]时,都有|f(x)|≤1,试求实数a的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时, ![]() .
.
(1)直接写出函数![]() 的增区间(不需要证明);
的增区间(不需要证明);
(2)求出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() (万元),若年产量不足
(万元),若年产量不足![]() 千件,
千件, ![]() 的图像是如图的抛物线,此时
的图像是如图的抛物线,此时![]() 的解集为
的解集为![]() ,且
,且![]() 的最小值是
的最小值是![]() ,若年产量不小于
,若年产量不小于![]() 千件,
千件, ![]() ,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com