
分析 (Ⅰ)利用AC是直径,所以BA⊥BC,或C、B均在坐标原点,由此求C点轨迹E的方程;
(Ⅱ)设直线AC的方程为y=kx+2,由$\left\{\begin{array}{l}y=kx+2\\{x^2}=8y\end{array}\right.$得:x2-8kx-16=0,利用韦达定理及对数的几何意义,证明QC⊥PQ,即可证明结论.
解答 (Ⅰ)解:设C点坐标为(x,y),则B点坐标为$({\frac{x}{2},0})$.
因为AC是直径,所以BA⊥BC,或C、B均在坐标原点.
因此$\overrightarrow{BA}•\overrightarrow{BC}$=(-$\frac{x}{2}$,2)•($\frac{x}{2}$,y)=0,
故有$\frac{x^2}{4}+2y=0$,即x2=8y,…3 分
另一方面,设$C({{x_0},\frac{x_0^2}{8}})$是曲线x2=8y上一点,
则有$AC=\sqrt{x_0^2+{{({\frac{x_0^2}{8}-2})}^2}}=\frac{x_0^2+16}{8}$,AC中点纵坐标为$\frac{{2+\frac{x_0^2}{8}}}{2}=\frac{x_0^2+16}{16}$,
故以AC为直径的圆与x轴相切.
综上可知C点轨迹E的方程为x2=8y. …(5分)
(Ⅱ)证明:设直线AC的方程为y=kx+2,
由$\left\{\begin{array}{l}y=kx+2\\{x^2}=8y\end{array}\right.$得:x2-8kx-16=0
设 C(x1,y1),P(x2,y2),则有x1x2=-16. …8 分
由$y=\frac{x^2}{8}$对x求导知$y'=\frac{x}{4}$,
从而曲线E在P处的切线斜率${k_2}=\frac{x_2}{4}$,
直线BC的斜率${k_1}=\frac{{\frac{x_1^2}{8}}}{{{x_1}-\frac{x_1}{2}}}=\frac{x_1}{4}$,…10 分
于是 ${k_1}{k_2}=\frac{{{x_1}{x_2}}}{16}=\frac{-16}{16}=-1$.
因此QC⊥PQ.
所以△PQC恒为直角三角形. …(12分)
点评 本题考查轨迹方程,考查直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 36π | B. | 28π | C. | 16π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
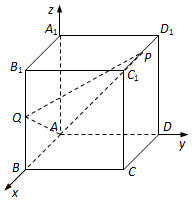 如图,在棱长为2的正方体ABCD-A1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0).
如图,在棱长为2的正方体ABCD-A1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
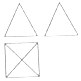 某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )
某四棱锥的三视图如图所示,正视图、侧视图都是边长为$2\sqrt{3}$的等边三角形,俯视图是一个正方形,则此四棱锥的体积是( )| A. | $8\sqrt{3}$ | B. | 12 | C. | 24 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com