
分析 根据抛物线方程可求得焦点坐标和准线方程,设过F的直线方程,与抛物线方程联立,整理后,设A(x1,y1),B(x2,y2)根据韦达定理可求得x1x2的值,又根据抛物线定义可知|AF|=x1+1,|BF|=x2+1代入 $\frac{1}{|AF|}$+$\frac{1}{|BF|}$可得其值为1,再由|AF|=4,即可得到|BF|.
解答 解:易知F坐标(1,0)准线方程为x=-1.
设过F点直线方程为y=k(x-1)
代入抛物线方程,得 k2(x-1)2=4x.
化简后为:k2x2-(2k2+4)x+k2=0.
设A(x1,y1),B(x2,y2)
则有x1x2=1
根据抛物线性质可知,|AF|=x1+1,|BF|=x2+1
∴$\frac{1}{|AF|}$+$\frac{1}{|BF|}$=$\frac{{x}_{1}+1+{x}_{2}+1}{({x}_{1}+1)({x}_{2}+1)}$=1,
又由$|{AF}|=\frac{4}{3}$,可得$\frac{3}{4}+\frac{1}{|BF|}=1$,则|BF|=4..
故答案为:4
点评 本题主要考查抛物线的应用和抛物线定义.对于过抛物线焦点的直线与抛物线关系,常用抛物线的定义来解决.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞$\frac{1}{3}$]∪[3,+∞) | B. | [$\frac{1}{3}$,3] | C. | [$\frac{1}{3}$,1] | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
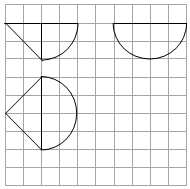 某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )
某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )| A. | $\frac{28}{3}π$ | B. | 4π | C. | $\frac{10}{3}π$ | D. | $\frac{2}{3}+\frac{8}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| y | 22 | 35 | 48 | 75 |
| A. | 22 | B. | 26 | C. | 33.6 | D. | 19.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{3π}{4}$或$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=N | B. | M?N | C. | M?N | D. | M∩N=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com