
分析 (Ⅰ)设出切点坐标,由$\left\{\begin{array}{l}{f({x}_{0})=0}\\{f′({x}_{0})=0}\end{array}\right.$即可求得a值,把a值代入函数解析式,得到当x变化时,f′(x)与f(x)的变化情况表,由图表可得f(x)的单调区间;
(Ⅱ)$\frac{f(x)}{x}>m(1-{e^x})$等价于$\left\{\begin{array}{l}{x<0}\\{f(x)<mx(1-{e}^{x})}\end{array}\right.$,或$\left\{\begin{array}{l}{x>0}\\{f(x)>mx(1-{e}^{x})}\end{array}\right.$,令g(x)=f(x)-mx(1-ex)=ln(x+1)-x-mx(1-ex),x∈(-1,+∞),求其二阶导数,然后对m分类讨论得答案.
解答 解:(Ⅰ)设切点为(x0,0),则f′(x)=$\frac{1}{x+a}-1$,
依题意$\left\{\begin{array}{l}{f({x}_{0})=0}\\{f′({x}_{0})=0}\end{array}\right.$,即$\left\{\begin{array}{l}{ln({x}_{0}+a)-{x}_{0}=0}\\{\frac{1}{{x}_{0}+a}-1=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{{x}_{0}=0}\end{array}\right.$.
∴f(x)=ln(x+1)-x,f′(x)=$\frac{-x}{x+1}$.
当x变化时,f′(x)与f(x)的变化情况如下表:
| x | (-1,0) | 0 | (0,+∞) |
| f′(x) | + | 0 | - |
| f(x) | 单调递增 | 极大值 | 单调递减 |
点评 本题主要考查导数的几何意义、导数及其应用、不等式等基础知识,考查推理论证能力、运算求解能力、创新意识等,考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想等,是压轴题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
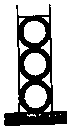 圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.
圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{e},0)∪(0,\frac{1}{e})$ | B. | $(-\frac{1}{2},0)∪(\frac{1}{2},1)$ | C. | $(-1,-\frac{1}{e})∪(\frac{1}{e},1)$ | D. | $(-1,-\frac{1}{2})∪(0,\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,e) | B. | (e,10] | C. | (1,10] | D. | (10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
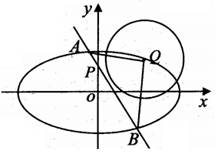 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,圆Q:x2+y2-4x-2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,圆Q:x2+y2-4x-2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com