
分析 (1)根据两点间的距离公式可知,两圆公共点的轨迹是一个椭圆;
(2)求出|MN|,P到直线lMN的距离的最大值,即可求△PMN面积的最大值.
解答 解:(1)曲线C上的点满足|PF1|+|PF2|=2$\sqrt{2}$>|F1F2|=2,∴曲线C是以F1,F2为焦点的椭圆
∴a=$\sqrt{2}$,c=1,b=1,
∴曲线C的方程是$\frac{x^2}{2}+{y^2}=1$-----------(4分)
(2)∵$\overrightarrow{{F}_{2}M}$=λ$\overrightarrow{{F}_{2}N}$=μ$\overrightarrow{a}$,∴M,N,F2三点共线,且直线lMN的斜率为$\sqrt{3}$
∴直线lMN的方程为$y=\sqrt{3}({x-1})$
与椭圆方程联立得7x2-12x+4=0
∴$|{MN}|=\sqrt{1+{k^2}}\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}$=$\frac{{8\sqrt{2}}}{7}$-----------(8分)
设$P({\sqrt{2}cosθ,sinθ})$,
∴P到直线lMN的距离$d=\frac{{|{\sqrt{6}cosθ-sinθ-\sqrt{3}}|}}{2}=\frac{{|{\sqrt{7}sin({θ+φ})-\sqrt{3}}|}}{2}$
∴${d_{max}}=\frac{{\sqrt{7}+\sqrt{3}}}{2}$,∴S△MNP的最大值为$\frac{{2\sqrt{14}+2\sqrt{6}}}{7}$-----------(12分)
点评 本题考查了圆的方程及其性质,椭圆的定义及直线与椭圆的位置关系及其处理方法,属于常规题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | y=±2x | C. | y=±3x | D. | y=±4x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,21-x>0 | |
| B. | ?a∈R,使函数y=xa的图象关于y轴对称 | |
| C. | ?a∈R,函数y=xa的图象经过第四象限 | |
| D. | ?x∈(0,+∞),使2x>x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 8 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
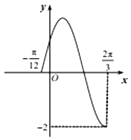 已知函数f(x)=2sin(ωx+φ),x∈[-$\frac{π}{12}$,$\frac{2π}{3}$]的图象如图所示,若f(x1)=f(x2),且x1≠x2,则f(x1+x2)的值为( )
已知函数f(x)=2sin(ωx+φ),x∈[-$\frac{π}{12}$,$\frac{2π}{3}$]的图象如图所示,若f(x1)=f(x2),且x1≠x2,则f(x1+x2)的值为( )| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | [-2,+∞) | C. | [1,2) | D. | (-2,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com