
| A. | m>0 | B. | m<0 | C. | m=0 | D. | m值与α有关 |
分析 由抛物线的定义及内错角相等,可得∠AFA1=∠A1FK,同理可证∠BFB1=∠B1FK,再利用平角为180°,即∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,∠A1FB1=90°,m=$\overrightarrow{F{A}_{1}}$$•\overrightarrow{F{B}_{1}}$=丨$\overrightarrow{F{A}_{1}}$丨•丨$\overrightarrow{F{A}_{2}}$丨cos∠A1FB1=0.
解答 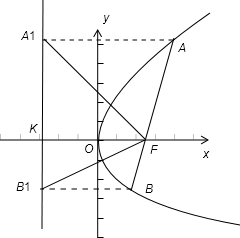 解:由题意可知:抛物线C:y2=4x,焦点坐标F(1,0),准线方程x=-1,
解:由题意可知:抛物线C:y2=4x,焦点坐标F(1,0),准线方程x=-1,
如图:设准线与x轴的交点为K,
∵A、B在抛物线的准线上的射影为A1、B1,
由抛物线的定义可得,丨AA1丨=丨AF丨,
∴∠AA1F=∠AFA1,
又由内错角相等可知:∠AA1F=∠A1FK,
∴∠AFA1=∠A1FK.
同理可证∠BFB1=∠B1 FK.
由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,
∴∠A1FK+∠B1FK=∠A1FB1=90°,
∴∠A1FB1=90°,
∵m=$\overrightarrow{F{A}_{1}}$$•\overrightarrow{F{B}_{1}}$=丨$\overrightarrow{F{A}_{1}}$丨•丨$\overrightarrow{F{A}_{2}}$丨cos∠A1FB1=0,
故选C.
点评 本题考查抛物线的简单性质,抛物线的定义,考查两条直线平行,内错角相等,考查向量的数量积,考查计算能力,属于中档题.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
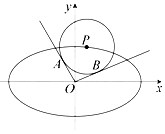 如图,已知P(x0,y0)是椭圆C:$\frac{x^2}{a^2}+{y^2}$=1上一点,过原点的斜率分别为k1,k2的两条直线与圆(x-x0)2+(y-y0)2=$\frac{4}{5}$分别相切于A,B两点.
如图,已知P(x0,y0)是椭圆C:$\frac{x^2}{a^2}+{y^2}$=1上一点,过原点的斜率分别为k1,k2的两条直线与圆(x-x0)2+(y-y0)2=$\frac{4}{5}$分别相切于A,B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com