



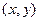 ,Q点不在原点,
,Q点不在原点,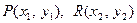
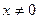 时
时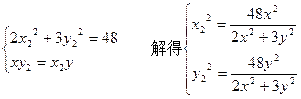
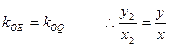
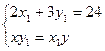
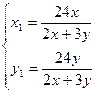

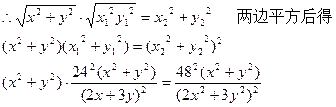
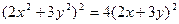
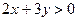
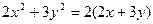
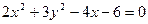
 可得Q(0,2),Q点满足这个方程
可得Q(0,2),Q点满足这个方程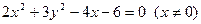
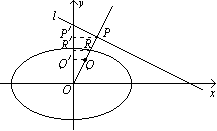 |
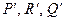
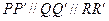

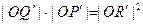
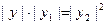
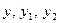 三个量同号
三个量同号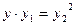
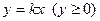
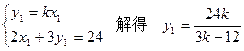
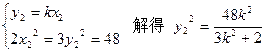
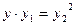 中
中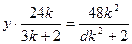
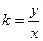
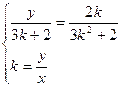
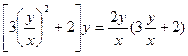
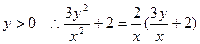
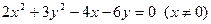 为所求的轨迹方程
为所求的轨迹方程 这样两个关系,又O、Q、R、P、D点共线,可以把P点、R点的坐标分别用动点Q的坐标表示后一起代入③④⑤
这样两个关系,又O、Q、R、P、D点共线,可以把P点、R点的坐标分别用动点Q的坐标表示后一起代入③④⑤ 中去整理。化简得轨迹方程;另外也可以过Q、R、P三点分别做y轴的垂线,将
中去整理。化简得轨迹方程;另外也可以过Q、R、P三点分别做y轴的垂线,将 转化成这三点纵坐标的关系,再求轨迹方程。本题解法一仍是坐标代换法的一种形式,主要是将动点的相关点的坐标用动点坐标表示后,代入联系着它们的等式中,求出动点的轨迹方程,这里因P点在直线l:
转化成这三点纵坐标的关系,再求轨迹方程。本题解法一仍是坐标代换法的一种形式,主要是将动点的相关点的坐标用动点坐标表示后,代入联系着它们的等式中,求出动点的轨迹方程,这里因P点在直线l: 上运动,而该直线与y轴可以相交,当P点在y轴上时,R、Q也相对确定成为定值,所以在解决这个问题时,先两步,第一部P在直线l上,运动不在y轴时(完全是“动态”)情况,第二步必须再看P在y轴时Q点做为定点是否符合所求的轨迹方程。这正是容易被忽略的,必须注意。
上运动,而该直线与y轴可以相交,当P点在y轴上时,R、Q也相对确定成为定值,所以在解决这个问题时,先两步,第一部P在直线l上,运动不在y轴时(完全是“动态”)情况,第二步必须再看P在y轴时Q点做为定点是否符合所求的轨迹方程。这正是容易被忽略的,必须注意。

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
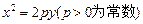 ,
,
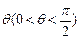 的直线交抛物线于
的直线交抛物线于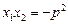
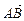 所成的比为
所成的比为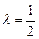 ,求直线AB的方程
,求直线AB的方程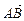 所成的比为
所成的比为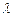 ,求
,求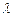 关于
关于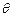 的函数关系式。
的函数关系式。 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
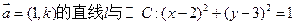 ,相交于M、N两点.
,相交于M、N两点.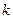 的取值范围;
的取值范围; 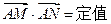 ;
;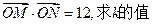 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com