
(本小题满分12分)
下列三个图中,左边是一个正方体截去一个角后所得多面体的直观图。右边两个是正视图和侧视图.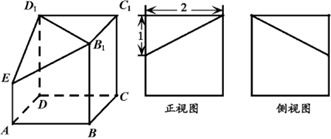
(1)请在正视图的下方,按照画三视图的要求画出该多面体的俯视图(不要求叙述作图过程);
(2)求该多面体的体积(尺寸如图).
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
某高速公路收费站入口处的安全标识墩如图1所示。墩的上半部分是正四棱锥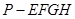 ,下半部分是长方体
,下半部分是长方体 。图2、图3分别是该标识墩的正(主)视图和俯视图。
。图2、图3分别是该标识墩的正(主)视图和俯视图。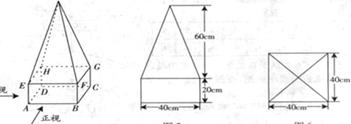
图1 图2 图3
(1)请在正视图右侧画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)一个四棱锥的直观图和三视图如图所示: 

(1)求证: ⊥
⊥ ;
;
(2)求出这个几何体的体积。
(3)若在PC上有一点E,满足CE:EP=2:1,求证PA//平面BED。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)如图,圆柱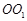 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.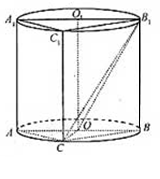
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)设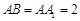 ,在圆柱
,在圆柱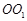 内随机选取一点,记该点取自于三棱柱
内随机选取一点,记该点取自于三棱柱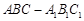 内的概率为
内的概率为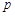 .
.
(ⅰ)当点C在圆周上运动时,求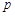 的最大值;
的最大值;
(ii)记平面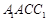 与平面
与平面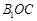 所成的角为
所成的角为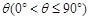 ,当
,当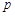 取最大值时,求
取最大值时,求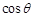 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
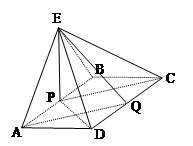
(本小题满分12分)如图,在四棱锥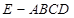 中,底面
中,底面 是矩形,
是矩形,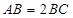 ,
,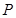 、
、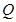 分别为线段
分别为线段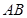 、
、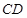 的中点,
的中点,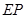 ⊥底面
⊥底面 .
.
(Ⅰ)求证: ∥平面
∥平面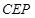 ;
;
(Ⅱ)求证:平面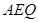 ^平面
^平面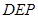 ;
;
(Ⅲ)若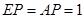 ,求三棱锥
,求三棱锥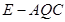 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知正方形ABCD的边长为1,FD⊥平面ABCD,EB⊥平面ABCD,FD=BE=1,M为BC边上的动点.试探究点M的位置,使F—AE—M为直二面角
.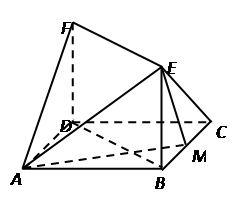
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com