
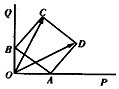
 如图,边长为2的正方形 A BCD的顶点 A,B分别在两条互相垂直的射线 OP,OQ上滑动,则$\overrightarrow{{O}C}•\overrightarrow{{O}D}$的最大值为( )
如图,边长为2的正方形 A BCD的顶点 A,B分别在两条互相垂直的射线 OP,OQ上滑动,则$\overrightarrow{{O}C}•\overrightarrow{{O}D}$的最大值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 令∠OAB=θ,由边长为2的正方形ABCD的顶点A、B分别在x轴、y轴正半轴上,可得出D,C的坐标,由此可以表示出两个向量,算出它们的数量积,通过三角函数的最值求解即可.
解答 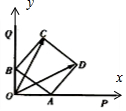 解:如图:令OP为x轴,OQ为y轴,∠OAB=θ,由于AB=2故0A=2cosθ,OB=2sinθ,
解:如图:令OP为x轴,OQ为y轴,∠OAB=θ,由于AB=2故0A=2cosθ,OB=2sinθ,
如图∠DAX=$\frac{π}{2}$-θ,AB=2,故xD=2cosθ+2cos($\frac{π}{2}$-θ)=2cosθ+2sinθ,yD=2sin($\frac{π}{2}$-θ)=2cosθ
故$\overrightarrow{OD}$=2(cosθ+sinθ,cosθ)
同理可求得C(2sinθ,2cosθ+2sinθ),即$\overrightarrow{OC}$=2(sinθ,cosθ+sinθ),
∴$\overrightarrow{OD}$•$\overrightarrow{OC}$=4(cosθ+sinθ,cosθ)•(sinθ,cosθ+sinθ)=4+4sin2θ,
$\overrightarrow{OD}$•$\overrightarrow{OC}$的最大值是8.
故选:D.
点评 本题考查向量在几何中的应用,设角引入坐标是解题的关键,由于向量的运算与坐标关系密切,所以在研究此类题时应该想到设角来表示点的坐标.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 结论正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com