练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．用反证法证明命题“设a，b为实数，则方程x3+ax2+b=0至少有一个实根”时，要做的假设是（　　）
    A．方程x3+ax2+b=0至多有一个实根B．方程x3+ax2+b=0没有实根
    C．方程x3+ax2+b=0至多有两个实根D．方程x3+ax2+b=0恰好有两个实根

    分析 直接利用命题的否定写出假设即可．

    解答 解：反证法证明问题时，反设实际是命题的否定，
    ∴用反证法证明命题“设a，b为实数，则方程x3+ax2+b=0至少有一个实根”时，要做的假设是：方程x3+ax2+b=0没有实根．
    故选：B．

    点评 本题考查反证法证明问题的步骤，基本知识的考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．（3x-$\frac{1}{2}$y）9的展开式中的偶数项的二项式系数之和为256．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知$|\overrightarrow a|$=1，$|\overrightarrow b|$=2，$\overrightarrow a$与$\overrightarrow b$的夹角为60°．求：
    （1）$|\overrightarrow a+\overrightarrow b|$，$|\overrightarrow a-\overrightarrow b|$
    （2）$\overrightarrow b$与$\overrightarrow a-\overrightarrow b$的夹角θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．下面几种推理中是演绎推理的是（　　）
    A．由金、银、铜、铁可导电，猜想：金属都可以导电
    B．猜想数列5，7，9，11，…的通项公式为an=2n+3
    C．半径为r的圆的面积S=π•r2，则单位圆的面积S=π
    D．由正三角形的性质得出正四面体的性质

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．求下列各式的值：
    （1）cos$\frac{25π}{3}$+tan（$\frac{15π}{4}$）；
    （2）sin810°+tan765°-cos360°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

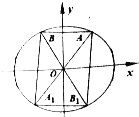    12．已知离心率为$\frac{1}{2}$的椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），右焦点到椭圆上的点的距离的最大值为3．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设点A，B是椭圆C上的两个动点，直线OA，OB与椭圆的另一交点分别为A1，B1，且直线OA，OB的斜率之积等于-$\frac{3}{4}$，问四边形ABA1B1的面积S是否为定值？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知圆的一般方程x2+y2-4x-2y-5=0，其半径是$\sqrt{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知f（x）=|x•ex|，又g（x）=f2（x）+tf（x）（t∈R），若满足g（x）=-1的x有四个，则t的取值范围为（　　）
    A．（-∞，-$\frac{{e}^{2}+1}{e}$）B．（$\frac{{e}^{2}+1}{e}$，+∞）C．（-$\frac{{e}^{2}+1}{e}$，-2）D．（2，$\frac{{e}^{2}+1}{e}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F2的直线交双曲线于A，B两点，连结AF1，BF1，若|AB|=|BF1|，且∠ABF1=90°，则双曲线的离心率为（　　）
    A．5-2$\sqrt{2}$B．$\sqrt{5-2\sqrt{2}}$C．6-3$\sqrt{2}$D．$\sqrt{6-3\sqrt{2}}$

    查看答案和解析>>

    同步练习册答案