练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．下面几种推理中是演绎推理的是（　　）
    A．由金、银、铜、铁可导电，猜想：金属都可以导电
    B．猜想数列5，7，9，11，…的通项公式为an=2n+3
    C．半径为r的圆的面积S=π•r2，则单位圆的面积S=π
    D．由正三角形的性质得出正四面体的性质

    分析 本题考查的是演绎推理的定义，判断一个推理过程是否是演绎推理关键是看他是否符合演绎推理的定义，能否从推理过程中找出“三段论”的三个组成部分．

    解答 解：选项A是由特殊到一般的推理过程，为归纳推理，
    选项B，是由特殊到一般的推理过程，为归纳推理
    选项C：半径为r圆的面积S=πr2，因为单位圆的半径为1，则单位圆的面积S=π中，
    半径为r圆的面积S=πr2，是大前提
    单位圆的半径为1，是小前提
    单位圆的面积S=π为结论；
    选项D是由特殊到与它类似的另一个特殊的推理过程，是类比推理，
    故选：C．

    点评 判断一个推理过程是否是归纳推理关键是看他是否符合归纳推理的定义，即是否是由特殊到一般的推理过程．
    判断一个推理过程是否是类比推理关键是看他是否符合类比推理的定义，即是否是由特殊到与它类似的另一个特殊的推理过程．
    判断一个推理过程是否是演绎推理关键是看他是否符合演绎推理的定义，能否从推理过程中找出“三段论”的三个组成部分．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．△ABC中，cosA=$\frac{1}{3}$，AB=2，则$\overrightarrow{CA}•\overrightarrow{CB}$的最小值是-$\frac{1}{9}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知椭圆Γ：$\frac{{a}^{2}}{{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点与短轴两端点构成一个面积为2的等腰直角三角形，O为坐标原点：
    （1）求椭圆Г的方程：
    （2）设点A在椭圆Г上，点B在直线y=2上，且OA⊥OB，求证：$\frac{1}{O{A}^{2}}$+$\frac{1}{O{B}^{2}}$为定值：
    （3）设点C在Γ上运动，OC⊥OD，且点O到直线CD距离为常数d（0＜d＜2），求动点D的轨迹方程：

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的两焦点为F1（-c，0），F2（c，0），椭圆的上顶点M满足$\overrightarrow{{F_1}M}$•$\overrightarrow{{F_2}M}$=0．
    （Ⅰ）求椭圆C的离心率e；
    （Ⅱ）若以点N（0，2）为圆心，且与椭圆C有公共点的圆的最大半径为$\sqrt{26}$．
    （ⅰ）求此时椭圆C的方程；
    （ⅱ）椭圆C上是否存在两点A，B关于直线l：y=kx-1（k≠0）对称，若存在，求出k的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

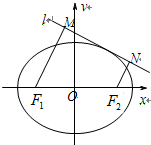    10．已知椭圆C的中心在坐标原点，左、右焦点分别为F1，F2，P为椭圆C上的动点，△PF1F2的面积最大值为$\sqrt{3}$，以原点为圆心，椭圆短半轴长为半径的圆与直线y=$\sqrt{3}$（x+2）相切．
    （1）求椭圆C的方程；
    （2）如图，动直线l：y=kx+m与椭圆C有且仅有一个公共点，点M，N是直线l上的两点，且F1M⊥l，F2M⊥l．求四边形F1MNF2面积S的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的上顶点M与左、右焦点F1、F2构成三角形MF1F2面积为$\sqrt{3}$，又椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$．
    （1）求椭圆C的方程；
    （2）椭圆C的下顶点为N，过点T（t，2）（t≠0）的直线TM，TN分别与椭圆C交于E，F两点．若△TMN的面积是△TEF的面积的k倍，求k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．用反证法证明命题“设a，b为实数，则方程x3+ax2+b=0至少有一个实根”时，要做的假设是（　　）
    A．方程x3+ax2+b=0至多有一个实根B．方程x3+ax2+b=0没有实根
    C．方程x3+ax2+b=0至多有两个实根D．方程x3+ax2+b=0恰好有两个实根

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在平面直角坐标系xOy中，动点P到定点F（1，0）的距离和它到定直线x=2的距离比是$\frac{\sqrt{2}}{2}$．
    （1）求动点P的轨迹C的方程；
    （2）设过点Q（$\frac{\sqrt{2}}{3}$，0）的直线l与曲线C交于点M，N，求证：点A（$\sqrt{2}$，0）在以MN为直经的圆上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}，0≤x＜1}\\{2-x，1≤x＜2}\\{2x-4，2≤x}\end{array}\right.$
    （1）求f（0），f（1），f（2），f（5）；
    （2）作出其图象；
    （3）求出其单调区间．

    查看答案和解析>>

    同步练习册答案