
分析 (Ⅰ)由$\overrightarrow{{F_1}M}$•$\overrightarrow{{F_2}M}$=0,得到b=c,由此能求出椭圆C的离心率.
(Ⅱ)①由设椭圆C的方程为$\frac{x^2}{{2{b^2}}}+\frac{y^2}{b^2}=1$.设P(x,y)是椭圆上任一点,|PN|的最大值为$\sqrt{26}$,则|PN|2=x2+(y-2)2=-(y+2)2+2b2+8(-b≤y≤b).由此能求出椭圆方程.
②设直线AB的方程为x=-ky+m,联立方程组$\left\{\begin{array}{l}{x^2}+2{y^2}=18\\ x=-ky+m\end{array}\right.$,得:(k2+2)y2-2kmy+m2-18=0,由此利用根的判别式、韦达定理、中点坐标、椭圆性质,能求出k的取值范围.
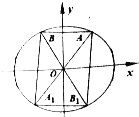
解答 解:(Ⅰ)∵$\overrightarrow{{F_1}M}$•$\overrightarrow{{F_2}M}$=(c,b)•(-c,b)=-c2+b2=0,
∴b=c,从而a=$\sqrt{2}$c,
∴椭圆C的离心率e=$\frac{c}{a}$=$\frac{{\sqrt{2}}}{2}$. …(3分)
(Ⅱ)①由(Ⅰ)可得椭圆C的方程为$\frac{x^2}{{2{b^2}}}+\frac{y^2}{b^2}=1$.
设P(x,y)是椭圆上任一点,依题意,|PN|的最大值为$\sqrt{26}$,
则|PN|2=x2+(y-2)2=(2b2-2y2)+(y-2)2=-(y+2)2+2b2+8(-b≤y≤b).
(ⅰ)若b≥2,则y=-2时,|PN|max=$\sqrt{2{b^2}+8}$=$\sqrt{26}$,
∴b=3,此时椭圆方程为$\frac{x^2}{18}+\frac{y^2}{9}=1$. …(7分)
(ⅱ)若0<b<2,则y=-b时,|PN|max=b+2=$\sqrt{26}$,
∴b=$\sqrt{26}$-2>2,矛盾.
综上得椭圆方程为$\frac{x^2}{18}+\frac{y^2}{9}=1$. …(9分)
②设直线AB的方程为x=-ky+m,
联立方程组$\left\{\begin{array}{l}{x^2}+2{y^2}=18\\ x=-ky+m\end{array}\right.$
化简得:(k2+2)y2-2kmy+m2-18=0,
由△=4k2m2-4(k2+2)(m2-18)>0,解得:9k2-m2+18>0.
由韦达定理得:yA+yB=$\frac{2km}{{{k^2}+2}}$,
可求得AB的中点坐标为($\frac{2m}{{{k^2}+2}}$,$\frac{km}{{{k^2}+2}}$),
代入直线y=kx-1得$\frac{km}{{{k^2}+2}}$=$\frac{2km}{{{k^2}+2}}$-1,求得m=$\frac{{{k^2}+2}}{k}$,
代入9k2-m2+18>0得9k2-${({\frac{{{k^2}+2}}{k}})^2}$+18>0,
解得k∈(-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞).…(14分)
点评 本题考查椭圆离心率的求法,考查椭圆方程的求法,考查满足条件的直线的斜率是否存在的判断与求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y1<y3<y2 | D. | y2<y1<y3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 由金、银、铜、铁可导电,猜想:金属都可以导电 | |
| B. | 猜想数列5,7,9,11,…的通项公式为an=2n+3 | |
| C. | 半径为r的圆的面积S=π•r2,则单位圆的面积S=π | |
| D. | 由正三角形的性质得出正四面体的性质 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知离心率为$\frac{1}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),右焦点到椭圆上的点的距离的最大值为3.
已知离心率为$\frac{1}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),右焦点到椭圆上的点的距离的最大值为3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某电子商务公司对1000名网络购物者2015年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为600.
某电子商务公司对1000名网络购物者2015年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为600.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com