
| A. | $[\frac{1}{3},\frac{{\sqrt{2}}}{2})$ | B. | $[\frac{{\sqrt{2}}}{3},\frac{{\sqrt{2}}}{2})$ | C. | $[\frac{{\sqrt{5}}}{6},\frac{{\sqrt{2}}}{2})$ | D. | $[\frac{{\sqrt{6}}}{7},\frac{{\sqrt{2}}}{2})$ |
分析 由题意AE=mAC(0≤m<1),AF=nAC(0<n<1),m+n=1,利用极值法讨论,当m=1,n=0以及n=1,m=0时,交点为B或C,此时AP<$\frac{\sqrt{2}}{2}$最大,求解EF=1,当m=n=$\frac{1}{2}$时,AP取得最小值,交点P为三角形的重心,求出即可得.
解答 解:由题意:等腰直角三角形ABC的斜边为$\sqrt{2}$,且AB⊥AC,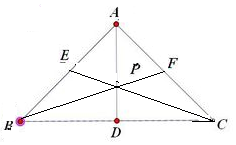
∴AB=AC=1,
∵E,F分别是AB,AC上的动点,AE=mAB(0≤m<1),AF=nAC(0<n<1),m+n=1,根据题意,当m=n=$\frac{1}{2}$时,AP取得最小值,此时E,F是各边的中点,故得交点P为三角形的重心.
由重心公式可得AP=$\frac{2}{3}×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{3}$,此时d=EF=$\frac{\sqrt{2}}{2}$,
∴AP•d的最小值为$\frac{1}{3}$.
当m=1,n=0以及n=1,m=0时,交点为B或C,此时AP<$\frac{\sqrt{2}}{2}$最大,此时d=EF=1,
∴AP•d的最大值小于$\frac{\sqrt{2}}{2}$.
故得AP•d的取值范围是[$\frac{1}{3}$,$\frac{\sqrt{2}}{2}$).
故选A.
点评 本题考查了等腰直角三角形的边角关系的应用问题,也考查了特殊值应用,极值法的运用.属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 16 | C. | 12 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com