
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
分析 利用复数代数形式的乘除运算化简,再由复数相等的条件列式求得a,b的值,则答案可求.
解答 解:∵$\frac{1+2i}{a+bi}=\frac{(1+2i)(a-bi)}{(a+bi)(a-bi)}$=$\frac{(a+2b)+(2a-b)i}{{a}^{2}+{b}^{2}}=1+i$,
∴$\left\{\begin{array}{l}{\frac{a+2b}{{a}^{2}+{b}^{2}}=1}\\{\frac{2a-b}{{a}^{2}+{b}^{2}}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=\frac{1}{2}}\end{array}\right.$.
∴a+b=$\frac{3}{2}+\frac{1}{2}=2$.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了复数相等的条件,是基础的计算题.


科目:高中数学 来源: 题型:选择题
| A. | {x|2≤x≤6} | B. | {x|2≤x≤5} | C. | {x|2<x<5} | D. | {x|1≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
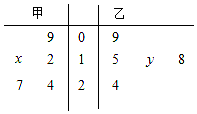 如图,茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x+y的值为( )
如图,茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x+y的值为( )| A. | 8 | B. | 10 | C. | 11 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂要安排生产Ⅰ、Ⅱ两种产品,这些产品要在A、B、C、D四种不同的设备上加工,按工艺规定,在一天内,产品Ⅰ每件在A、B、C、D设备上需要加工时间分别是2、2、3、0小时,产品Ⅱ每件在A、B、C、D设备上需要加工时间分别是4、1、0、3小时,A、B、C、D设备最长使用时间分别是16、8、9、9小时.设计划每天生产产品Ⅰ的数量为x(件),产品Ⅱ的数量为y(件).(x,y∈N)
某工厂要安排生产Ⅰ、Ⅱ两种产品,这些产品要在A、B、C、D四种不同的设备上加工,按工艺规定,在一天内,产品Ⅰ每件在A、B、C、D设备上需要加工时间分别是2、2、3、0小时,产品Ⅱ每件在A、B、C、D设备上需要加工时间分别是4、1、0、3小时,A、B、C、D设备最长使用时间分别是16、8、9、9小时.设计划每天生产产品Ⅰ的数量为x(件),产品Ⅱ的数量为y(件).(x,y∈N)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{{5\sqrt{2}}}{8}$ | D. | $\frac{{\sqrt{2}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com