
 某工厂要安排生产Ⅰ、Ⅱ两种产品,这些产品要在A、B、C、D四种不同的设备上加工,按工艺规定,在一天内,产品Ⅰ每件在A、B、C、D设备上需要加工时间分别是2、2、3、0小时,产品Ⅱ每件在A、B、C、D设备上需要加工时间分别是4、1、0、3小时,A、B、C、D设备最长使用时间分别是16、8、9、9小时.设计划每天生产产品Ⅰ的数量为x(件),产品Ⅱ的数量为y(件).(x,y∈N)
某工厂要安排生产Ⅰ、Ⅱ两种产品,这些产品要在A、B、C、D四种不同的设备上加工,按工艺规定,在一天内,产品Ⅰ每件在A、B、C、D设备上需要加工时间分别是2、2、3、0小时,产品Ⅱ每件在A、B、C、D设备上需要加工时间分别是4、1、0、3小时,A、B、C、D设备最长使用时间分别是16、8、9、9小时.设计划每天生产产品Ⅰ的数量为x(件),产品Ⅱ的数量为y(件).(x,y∈N)分析 (1)直接利用已知条件列出不等式组,画出可行域即可.
(2)写出目标函数,利用目标函数的几何意义求解函数的最值即可.
解答 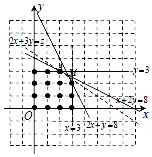 解:(1)x,y所满足的关系式为$\left\{\begin{array}{l}2x+4y≤16\\ 2x+y≤8\\ 0≤3x≤9\\ 0≤3y≤9\\ x,y∈N\end{array}\right.$,即$\left\{\begin{array}{l}x+2y≤8\\ 2x+y≤8\\ 0≤x≤3\\ 0≤y≤3\\ x,y∈N\end{array}\right.$.…(3分)
解:(1)x,y所满足的关系式为$\left\{\begin{array}{l}2x+4y≤16\\ 2x+y≤8\\ 0≤3x≤9\\ 0≤3y≤9\\ x,y∈N\end{array}\right.$,即$\left\{\begin{array}{l}x+2y≤8\\ 2x+y≤8\\ 0≤x≤3\\ 0≤y≤3\\ x,y∈N\end{array}\right.$.…(3分)
画出不等式组$\left\{\begin{array}{l}x+2y≤8\\ 2x+y≤8\\ 0≤x≤3\\ 0≤y≤3\\ x,y∈N\end{array}\right.$所表示的平面区域,即可行域,
(图中实心点)(注:可行域画成阴影区域及未标注x,y∈N扣1分)…(6分)
(2)设最大利润为z(万元),则目标函数z=2x+3y.…(8分)
将z=2x+3y变形$y=-\frac{2}{3}x+\frac{z}{3}$,这是斜率为$-\frac{2}{3}$,随z变化的一组平行直线,$\frac{z}{3}$是直线在y轴上的截距,
当$\frac{z}{3}$取得最大值时,z的值最大,又因为x,y所满足的约束条件,联立方程组$\left\{\begin{array}{l}x+2y=8\\ 2x+y=8\end{array}\right.$,得点M坐标为$({\frac{8}{3},\frac{8}{3}})$.
又∵x,y∈N,当直线$y=-\frac{2}{3}x+\frac{z}{3}$经过可行域上的点A(2,3)时,截距$\frac{z}{3}$最大.…(10分)
此时,z=2×2+3×3=13.
所以,每天安排生产2件产品Ⅰ,3件产品Ⅱ,会使利润最大为13(万元).…(12分)
点评 本题考查线性规划的简单应用,考查数形结合思想以及转化思想的应用,考查计算能力.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $[{0,\frac{12}{5}}]$ | B. | [0,1] | C. | $[{1,\frac{12}{5}}]$ | D. | $({0,\frac{12}{5}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,5} | B. | {2,5,7,8} | C. | {2,3,5,6,7,8} | D. | {1,2,3,4,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
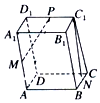 如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )| A. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{3}{2}\overrightarrow c$ | B. | $\overrightarrow a+\frac{1}{2}\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com