
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}+{y^2}=1$ | B. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ | C. | $\frac{x^2}{12}+\frac{y^2}{4}=1$ | D. | $\frac{x^2}{12}+\frac{y^2}{8}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| B. | 向右平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| C. | 向左平移$\frac{π}{2}$个单位,再向下平移1个单位 | |
| D. | 向右平移$\frac{π}{2}$个单位,再向上平移1个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
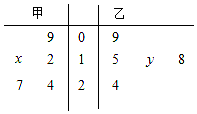 如图,茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x+y的值为( )
如图,茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x+y的值为( )| A. | 8 | B. | 10 | C. | 11 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 285 | B. | 286 | C. | 287 | D. | 288 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂要安排生产Ⅰ、Ⅱ两种产品,这些产品要在A、B、C、D四种不同的设备上加工,按工艺规定,在一天内,产品Ⅰ每件在A、B、C、D设备上需要加工时间分别是2、2、3、0小时,产品Ⅱ每件在A、B、C、D设备上需要加工时间分别是4、1、0、3小时,A、B、C、D设备最长使用时间分别是16、8、9、9小时.设计划每天生产产品Ⅰ的数量为x(件),产品Ⅱ的数量为y(件).(x,y∈N)
某工厂要安排生产Ⅰ、Ⅱ两种产品,这些产品要在A、B、C、D四种不同的设备上加工,按工艺规定,在一天内,产品Ⅰ每件在A、B、C、D设备上需要加工时间分别是2、2、3、0小时,产品Ⅱ每件在A、B、C、D设备上需要加工时间分别是4、1、0、3小时,A、B、C、D设备最长使用时间分别是16、8、9、9小时.设计划每天生产产品Ⅰ的数量为x(件),产品Ⅱ的数量为y(件).(x,y∈N)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com