
| A. | 向左平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| B. | 向右平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| C. | 向左平移$\frac{π}{2}$个单位,再向下平移1个单位 | |
| D. | 向右平移$\frac{π}{2}$个单位,再向上平移1个单位 |
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:解答题
| x | -$\frac{π}{6}$ | $\frac{π}{3}$ | $\frac{5π}{6}$ | $\frac{4π}{3}$ | $\frac{11π}{6}$ |
| ωx+φ | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ |
| y | -1 | 1 | 3 | 1 | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}}]$ | B. | (0,3] | C. | $[{\frac{1}{2},3}]$ | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | 4π | C. | 6π | D. | $\frac{9π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
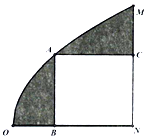 某校一块空地的轮廓线如图所示,曲线段OM是以O为顶点,ON为对称轴且开口向右的抛物线的一段,已知ON=4(单位:百米),MN=4.现计划在该区域内围出一块矩形地块ABNC作为学生活动区域,其余阴影部分进行绿化建设,其中A在曲线段OM上,C在MN上,B在ON上.
某校一块空地的轮廓线如图所示,曲线段OM是以O为顶点,ON为对称轴且开口向右的抛物线的一段,已知ON=4(单位:百米),MN=4.现计划在该区域内围出一块矩形地块ABNC作为学生活动区域,其余阴影部分进行绿化建设,其中A在曲线段OM上,C在MN上,B在ON上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com