Question

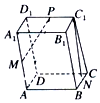
10．如图所示，在平行六面体ABCD-A₁B₁C₁D₁中，设$\overrightarrow{A{A_1}}=\overrightarrow a$，$\overrightarrow{AB}=\overrightarrow b$，$\overrightarrow{AD}=\overrightarrow c$，M，N，P分别是AA₁，BC，C₁D₁的中点，则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=（　　）

• A． $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{3}{2}\overrightarrow c$
• B． $\overrightarrow a+\frac{1}{2}\overrightarrow c$
• C． $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$
• D． $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$

Answer 1

分析 根据空间向量的线性表示，用$\overrightarrow{{AA}_{1}}$、$\overrightarrow{AD}$和$\overrightarrow{AB}$分别表示出$\overrightarrow{MP}$和$\overrightarrow{{NC}_{1}}$，求和即可．

解答 解：平行六面体ABCD-A₁B₁C₁D₁中，$\overrightarrow{A{A_1}}=\overrightarrow a$，$\overrightarrow{AB}=\overrightarrow b$，$\overrightarrow{AD}=\overrightarrow c$，
M，N，P分别是AA₁，BC，C₁D₁的中点，
∴$\overrightarrow{MP}$=$\overrightarrow{{MA}_{1}}$+$\overrightarrow{{{A}_{1}D}_{1}}$+$\overrightarrow{{D}_{1}P}$
=$\frac{1}{2}$$\overrightarrow{{AA}_{1}}$+$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{AB}$
=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{c}$+$\frac{1}{2}$$\overrightarrow{b}$，
$\overrightarrow{{NC}_{1}}$=$\overrightarrow{NC}$+$\overrightarrow{{CC}_{1}}$
=$\frac{1}{2}$$\overrightarrow{AD}$+$\overrightarrow{{AA}_{1}}$
=$\frac{1}{2}$$\overrightarrow{c}$+$\overrightarrow{a}$；
∴$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=（$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$）+（$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{c}$）
=$\frac{3}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{3}{2}$$\overrightarrow{c}$．
故选：A．

点评 本题考查了空间向量的线性表示与应用问题，是基础题目．