
���� ��1������sin2��+cos2��=1��ȥֱ��l�IJ����ɵ���ͨ���̣���x=��cos�ȣ�y=��sin�ȣ��ɵü����귽�̣�
��2���������$��=\frac{��}{6}$���ɼ����귽�̦�=2cos�ȵ�${��_1}=\sqrt{3}$����ֱ�ߵļ����귽��$2��sin��{��+\frac{��}{3}}��=6\sqrt{3}$��${��_2}=3\sqrt{3}$
���ü����귽�̼�������ɵ��߶�PQ�ij���
��� �⣺��1��ԲC�IJ�������Ϊ$\left\{\begin{array}{l}x=1+cos��\\ y=sin��\end{array}$������Ϊ��������
��cos��=x-1��sin��=y��
��sin2��+cos2��=1���ɵã�x-1��2+y2=1��
��ԲC����ͨ����Ϊ��x-1��2+y2=1��
�֡�x=��cos�ȣ�y=��sin�ȣ�����ԲC�ļ����귽��Ϊ��=2cos�ȣ�
��2���������$��=\frac{��}{6}$���ɼ����귽�̦�=2cos�ȣ���${��_1}=\sqrt{3}$��
��ֱ�ߵļ����귽��$2��sin��{��+\frac{��}{3}}��=6\sqrt{3}$����${��_2}=3\sqrt{3}$
�����귽�̼�������ɵ��߶�PQ�ij���$PQ=|{{��_1}-{��_2}}|=2\sqrt{3}$��
���� ���⿼���ļ������ֱ������Ļ������Լ�����ƽ�漸��֪ʶ������⣮����ֱ�������뼫�����Ĺ�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
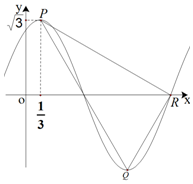 ��֪����f��x��=Asin����x+�գ���A��0���أ�0�����䲿��ͼ����ͼ��ʾ����P��Q�ֱ�Ϊͼ�������ڵ���ߵ�����͵㣬R��ͼ����x��Ľ��㣬��P��ĺ�����Ϊ$\frac{1}{3}$��f��$\frac{1}{3}$��=$\sqrt{3}$��PR��QR������f��x���Ľ���ʽ�����ǣ�������
��֪����f��x��=Asin����x+�գ���A��0���أ�0�����䲿��ͼ����ͼ��ʾ����P��Q�ֱ�Ϊͼ�������ڵ���ߵ�����͵㣬R��ͼ����x��Ľ��㣬��P��ĺ�����Ϊ$\frac{1}{3}$��f��$\frac{1}{3}$��=$\sqrt{3}$��PR��QR������f��x���Ľ���ʽ�����ǣ�������| A�� | $f��x��=\sqrt{3}sin��\frac{��}{2}x+\frac{��}{3}��$ | B�� | $f��x��=\sqrt{3}sin��\frac{��}{2}x-\frac{��}{6}��$ | ||
| C�� | $f��x��=\sqrt{3}sin��\frac{2��}{3}x+\frac{5��}{18}��$ | D�� | $f��x��=\sqrt{3}sin����x+\frac{��}{6}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-$\frac{{y}^{2}}{4}$=1 | B�� | x2-$\frac{{y}^{2}}{3}$=1 | C�� | x2-$\frac{{y}^{2}}{5}$=1 | D�� | x2-$\frac{{y}^{2}}{6}$=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3��+�ޣ� | B�� | [3��+�ޣ� | C�� | ��-�ޣ�3�� | D�� | ��-�ޣ�3] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2-ln2 | B�� | 2ln2-$\frac{1}{2}$ | C�� | 2+ln2 | D�� | 2ln2+$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��2��3} | B�� | {1��3} | C�� | ��1��3] | D�� | ��1��5] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-1��0��1} | B�� | {0��1} | C�� | [0��1] | D�� | [-1��1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | 1 | C�� | $\frac{2}{3}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com