
| A. | [$\sqrt{2}$,+∞) | B. | (1,$\frac{\sqrt{5}}{2}$] | C. | [$\frac{\sqrt{5}+1}{2}$,+∞) | D. | [$\frac{\sqrt{10}+\sqrt{2}}{4}$,+∞) |
分析 设P(m,n),即有$\frac{{m}^{2}}{{a}^{2}}$-$\frac{{n}^{2}}{{b}^{2}}$=1,运用两点的距离公式,可得2b=$\sqrt{{m}^{2}+(n-b)^{2}}$,转化为n的函数,由配方可得最小值,由离心率公式,解不等式可得e的范围.
解答 解:设P(m,n),即有$\frac{{m}^{2}}{{a}^{2}}$-$\frac{{n}^{2}}{{b}^{2}}$=1,
由|AB|=|BP|,可得2b=$\sqrt{{m}^{2}+(n-b)^{2}}$,
即有4b2=a2(1+$\frac{{n}^{2}}{{b}^{2}}$)+(n-b)2,
即为3b2-a2=$\frac{{c}^{2}}{{b}^{2}}$n2-2bn=$\frac{{c}^{2}}{{b}^{2}}$(n-$\frac{{b}^{3}}{{c}^{2}}$)2-$\frac{{b}^{4}}{{c}^{2}}$,
即有3b2-a2≥-$\frac{{b}^{4}}{{c}^{2}}$,
即为(3c2-4a2)c2+(c2-a2)2≥0,
化简可得4c4-6a2c2+a4≥0,
由e=$\frac{c}{a}$可得4e4-6e2+1≥0,(e>1),
解得e2≥$\frac{3+\sqrt{5}}{4}$,即为e≥$\frac{\sqrt{10}+\sqrt{2}}{4}$.
故选:D.
点评 本题考查双曲线的离心率的范围,注意运用二次函数的最值的求法,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
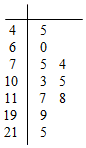 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;>300为严重污染.
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;>300为严重污染.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{19}{5}$ | B. | $-\frac{5}{19}$ | C. | $-\frac{31}{17}$ | D. | $-\frac{17}{31}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M<N<P<Q | B. | P<Q<M<N | C. | N<M<Q<P | D. | Q<P<N<M |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
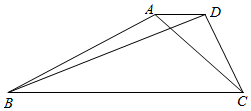 如图,在梯形ABCD中,已知AD∥BC,AD=1,BD=2$\sqrt{10}$,∠CAD=$\frac{π}{4}$,tan∠ADC=-2,求:
如图,在梯形ABCD中,已知AD∥BC,AD=1,BD=2$\sqrt{10}$,∠CAD=$\frac{π}{4}$,tan∠ADC=-2,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com