
| A. | $-\frac{19}{5}$ | B. | $-\frac{5}{19}$ | C. | $-\frac{31}{17}$ | D. | $-\frac{17}{31}$ |
分析 由题意和同角三角函数基本关系和二倍角公式可得tan2α,再由两角和的正切公式代入计算可得.
解答 解:∵$sinα=\frac{3}{5}$,且α为第二象限角,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{4}{5}$,
∴tanα=$\frac{sinα}{cosα}$=-$\frac{3}{4}$,
∴tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=-$\frac{24}{7}$,
∴$tan({2α+\frac{π}{4}})$=$\frac{tan2α+1}{1-tan2α}$=-$\frac{17}{31}$,
故选:D.
点评 本题考查三角函数化简求值,涉及同角三角函数基本关系和二倍角公式以及两角和的正切公式,属基础题.


科目:高中数学 来源: 题型:选择题
| A. | “两个全等三角形的周长相等”的逆命题 | |
| B. | “若一个整数的末位数字是0,则这个整数能被2整除”的否命题 | |
| C. | “对顶角相等”的逆否命题 | |
| D. | ?x0∈R,x02-x0+1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
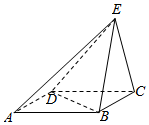 如图,ABCD是平行四边形,已知$AB=2BC=4,BD=2\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知$AB=2BC=4,BD=2\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{2}$,+∞) | B. | (1,$\frac{\sqrt{5}}{2}$] | C. | [$\frac{\sqrt{5}+1}{2}$,+∞) | D. | [$\frac{\sqrt{10}+\sqrt{2}}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com