
分析 (1)由椭圆定义得$|{P{F_1}}|+|{P{F_2}}|=2\sqrt{5}=2a$,由${|{{F_1}{F_2}}|^2}+{|{P{F_1}}|^2}={|{P{F_2}}|^2}$,得c=2,由此能求出椭圆方程.
(2)当直线L的斜率不存在时,直线L为x=0,DN=1,DM=3,$λ=\frac{1}{3}$;当直线L的斜率存在时,设直线L的方程为y=kx+2,代入$\frac{x^2}{5}+{y^2}=1$,得(1+5k2)x2+20kx+15=0,由此利用根的判别式、韦达定理、向量知识,结合已知条件能求出λ的取值范围.
解答 解:(1)∵椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点分别为F1,F2,点P在椭圆C上,
满足$\overrightarrow{P{F_1}}•\overrightarrow{{F_1}{F_2}}=0,|{\overrightarrow{P{F_1}}}|=\frac{{\sqrt{5}}}{5},|{\overrightarrow{P{F_2}}}|=\frac{{9\sqrt{5}}}{5}$.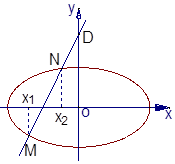
∴$|{P{F_1}}|+|{P{F_2}}|=2\sqrt{5}=2a$,得$a=\sqrt{5}$,由${|{{F_1}{F_2}}|^2}+{|{P{F_1}}|^2}={|{P{F_2}}|^2}$
得c=2,
由c2=a2-b2得b=1,
∴椭圆方程为$\frac{x^2}{5}+{y^2}=1$.…(4分)
(2)由题意可知:
当直线L的斜率不存在时,直线L为x=0,DN=1,DM=3,$λ=\frac{1}{3}$;…(6分)
当直线L的斜率存在时,设直线L的方程为y=kx+2,代入$\frac{x^2}{5}+{y^2}=1$,
得(1+5k2)x2+20kx+15=0,
△=(20k)2-4×15(1+5k2)>0,得k2>$\frac{3}{5}$,
设M(x1,y1),N(x2,y2),则$\left\{\begin{array}{l}{x_1}+{x_2}=-\frac{20k}{{1+5{k^2}}}\\{x_1}•{x_2}=\frac{15}{{1+5{k^2}}}\end{array}\right.$,….(8分)
由$\overrightarrow{DN}=λ\overrightarrow{DM}$得(x2,y2-2)=λ(x1,y1-2)
∴x2=λx1代入上式得$\left\{\begin{array}{l}{(1+λ)^2}{x_1}^2=\frac{{400{k^2}}}{{{{(1+5{k^2})}^2}}}\\ λ{x_1}^2=\frac{15}{{1+5{k^2}}}\end{array}\right.$再消去${x_1}^2$,得$\frac{{{{(1+λ)}^2}}}{λ}=\frac{{400{k^2}}}{{15(1+5{k^2})}}=\frac{80}{{3(5+\frac{1}{k^2})}}$,
∵${k^2}>\frac{3}{5}$,∴$0<\frac{1}{k^2}<\frac{5}{3}$,∴$5<\frac{1}{k^2}+5<\frac{20}{3}$,即$4<\frac{80}{{3(\frac{1}{k^2}+5)}}<\frac{16}{3}$,
∴$4<\frac{{{{(1+λ)}^2}}}{λ}<\frac{16}{3}$,解得$\frac{1}{3}<λ<3$,…(10分)
又N在D,M之间,∴$\frac{1}{3}<λ<1$,…(11分)
由上综合可得$\frac{1}{3}≤λ<1$.…(12分)
点评 本题考查椭圆方程、实数的取值范围的求法,是中档题,解题时要认真审题,注意椭圆性质、根的判别式、韦达定理、向量知识的合理运用.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:解答题
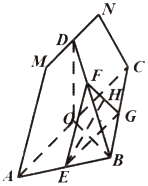 如图所示,四边形AMNC为等腰梯形,△ABC为直角三角形,平面AMNC与平面ABC垂直,AB=BC,AM=CN,点O、D、E分别是AC、MN、AB的中点.过点E作平行于平面AMNC的截面分别交BD、BC于点F、G,H是FG的中点.
如图所示,四边形AMNC为等腰梯形,△ABC为直角三角形,平面AMNC与平面ABC垂直,AB=BC,AM=CN,点O、D、E分别是AC、MN、AB的中点.过点E作平行于平面AMNC的截面分别交BD、BC于点F、G,H是FG的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
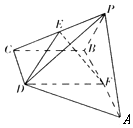 如图,在四棱锥P-ABCD中底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=2CD,BC=$\sqrt{3}$CD,△APB是等边三角形,且侧面APB⊥底面ABCD,E,F分别是PC,AB的中点.
如图,在四棱锥P-ABCD中底面ABCD是直角梯形,AB∥CD,∠ABC=90°,AB=2CD,BC=$\sqrt{3}$CD,△APB是等边三角形,且侧面APB⊥底面ABCD,E,F分别是PC,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{7}+\sqrt{3}}{2}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,以BD为直径的圆O经过A,C两点,延长DA,CB交于P点,如图2,将PAB沿线段AB折起,使P点在底面ABCD的射影恰为AD的中点Q,AB=BC=1,BD=2,线段PB,PC的中点为E,F.
如图1,以BD为直径的圆O经过A,C两点,延长DA,CB交于P点,如图2,将PAB沿线段AB折起,使P点在底面ABCD的射影恰为AD的中点Q,AB=BC=1,BD=2,线段PB,PC的中点为E,F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com