
分析 作出区域D,直线y-2=a(x+2)表示过点A(-2,2)且斜率为a的直线,数形结合可得结果.
解答 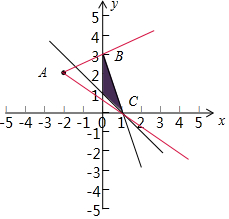 解:作出不等式组$\left\{\begin{array}{l}{x≥0}\\{x+y≥1}\\{3x+y≤3}\end{array}\right.$所对应的可行域D(如图阴影),
解:作出不等式组$\left\{\begin{array}{l}{x≥0}\\{x+y≥1}\\{3x+y≤3}\end{array}\right.$所对应的可行域D(如图阴影),
直线y-2=a(x+2)表示过点A(-2,2)且斜率为a的直线,
联立$\left\{\begin{array}{l}{x+y=1}\\{3x+y=3}\end{array}\right.$可解得即C(1,0),
由斜率公式可得a=$\frac{0-2}{1+2}$=$-\frac{2}{3}$,
由$\left\{\begin{array}{l}{x=0}\\{3x+y=3}\end{array}\right.$解得B(0,3),
此时A=$\frac{3-2}{0+2}$=$\frac{1}{2}$
结合图象可得要使直线y-2=a(x+2)与区域D有公共点需$-\frac{2}{3}≤$a≤$\frac{1}{2}$,
故答案为:$-\frac{2}{3}≤$a≤$\frac{1}{2}$.
点评 本题考查简单线性规划,数形结合是解决问题的关键,属中档题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:选择题
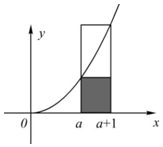 如图所示,由直线x=a,x=a+1(a>0),y=x2及 x 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即 a2<$\int_a^{a+1}{\;}$x2dx<(a+1)2.类比之,若对?n∈N*,不等式$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )
如图所示,由直线x=a,x=a+1(a>0),y=x2及 x 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即 a2<$\int_a^{a+1}{\;}$x2dx<(a+1)2.类比之,若对?n∈N*,不等式$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )| A. | ln$\frac{5}{2}$ | B. | ln 2 | C. | $\frac{1}{2}$ln 2 | D. | $\frac{1}{2}$ln 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(2x+$\frac{5π}{12}$) | B. | y=sin($\frac{x}{2}$+$\frac{5π}{12}$) | C. | y=sin ($\frac{x}{2}$-$\frac{π}{12}$) | D. | y=sin($\frac{x}{2}$+$\frac{5π}{24}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,3) | C. | (-1,1) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
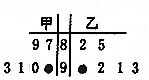 在学校组织的“环保知识”竞赛活动中,甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损,如图:
在学校组织的“环保知识”竞赛活动中,甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损,如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=200x | B. | y=100x2+100x | C. | y=100×2x | D. | y=0.2x+log2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com