
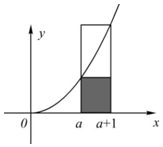
 如图所示,由直线x=a,x=a+1(a>0),y=x2及 x 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即 a2<$\int_a^{a+1}{\;}$x2dx<(a+1)2.类比之,若对?n∈N*,不等式$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )
如图所示,由直线x=a,x=a+1(a>0),y=x2及 x 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即 a2<$\int_a^{a+1}{\;}$x2dx<(a+1)2.类比之,若对?n∈N*,不等式$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )| A. | ln$\frac{5}{2}$ | B. | ln 2 | C. | $\frac{1}{2}$ln 2 | D. | $\frac{1}{2}$ln 5 |
分析 令A=A1+A2+A3+…+An,根据定积分的定义得到:A1=-lnn+ln(n+1),同理求出A2,A3,…,An的值,相加求出即可.
解答 解:令A=A1+A2+A3+…+An,
由题意得:$\frac{1}{n+1}$<A1<$\frac{1}{n}$,$\frac{1}{n+2}$<A2<$\frac{1}{n+1}$,$\frac{1}{n+3}$<A3<$\frac{1}{n+2}$,…,$\frac{1}{2n}$<An<$\frac{1}{2n-1}$,
∴A1=${∫}_{n}^{n+1}\frac{1}{x}$dx=lnx|${\;}_{n}^{n+1}$=ln(n+1)-lnn,
同理:A2=-ln(n+1)+ln(n+2),A3=-ln(n+2)+ln(n+3),…,An=-ln(2n-1)+ln2n,
∴A=A1+A2+A3+…+An
=-lnn+ln(n+1)-ln(n+1)+ln(n+2)-ln(n+2)+ln(n+3)-…-ln(2n-1)+ln2n
=ln2n-lnn
=ln2,
故选:B.
点评 本题考察了定积分的简单应用,根据定积分的定义得到A1,A2,A3,…,An的值是解题的关键,本题是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 30.4<40.2<log0.40.5 | B. | ${3^{0.4}}<{log_{0.4}}0.5<{4^{0.2}}$ | ||
| C. | ${log_{0.4}}0.5<{3^{0.4}}<{4^{0.2}}$ | D. | ${log_{0.4}}0.5<{4^{0.2}}<{3^{0.4}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
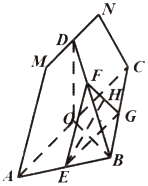 如图所示,四边形AMNC为等腰梯形,△ABC为直角三角形,平面AMNC与平面ABC垂直,AB=BC,AM=CN,点O、D、E分别是AC、MN、AB的中点.过点E作平行于平面AMNC的截面分别交BD、BC于点F、G,H是FG的中点.
如图所示,四边形AMNC为等腰梯形,△ABC为直角三角形,平面AMNC与平面ABC垂直,AB=BC,AM=CN,点O、D、E分别是AC、MN、AB的中点.过点E作平行于平面AMNC的截面分别交BD、BC于点F、G,H是FG的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com