
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①,x2f(x1)>x1f(x2)可变为$\frac{f({x}_{1})}{{x}_{1}}>\frac{f({x}_{2})}{{x}_{2}}$;原命题等价于,在函数f(x)图象上任一点A(x1,f(xx1)),都存在点B(x2,f(x2)),使得直线OA的斜率大于OB的斜率,结合图象可判定.
②,f(x1)-f(x2)<x2-x1可变为f(x1)+x1)<f(x2)+x2,原命题等价于,函数g(x)=f(x)+x,对?x2∈(0,+∞),都存在x1∈(0,+∞)使g(x2)>g(x1),根据函数g(x)有无最小值判定;
③,f(a+x)<f(a)•ex?(a+x)ln(a+x)<alna)•ex?$\frac{(a+x)ln(a+x)}{{e}^{a+x}}<\frac{alna}{{e}^{a}}$,构造函数g(x)=$\frac{xlnx}{{e}^{x}}$,利用导数判定函数g(x)=$\frac{xlnx}{{e}^{x}}$在区间(3,+∞)上的单调性即可
④,构造函数h(x)=f(x)f(a)-f′(a)(x-a)=xlnx-xlna-x+a,(x>3)利用导数判定h(x)单调性,求出最值即可判定.
解答 解:函数的定义域为(0,+∞),∵f′(x)=lnx+1,令lnx+1<0得0<x<$\frac{1}{e}$,
∴函数f(x)=xlnx的单调递减区间是( 0,$\frac{1}{e}$),单调增区间为($\frac{1}{e}$,+∞).
其大致图象如下: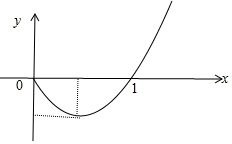
对于①,x2f(x1)>x1f(x2)可变为$\frac{f({x}_{1})}{{x}_{1}}>\frac{f({x}_{2})}{{x}_{2}}$;
原命题等价于,在函数f(x)图象上任一点A(x1,f(xx1)),都存在点B(x2,f(x2)),使得直线OA的斜率大于OB的斜率,结合图象可判定①正确.
对于②,f(x1)-f(x2)<x2-x1可变为f(x1)+x1)<f(x2)+x2,原命题等价于,函数g(x)=f(x)+x,对?x2∈(0,+∞),都存在x1∈(0,+∞)使g(x2)>g(x1);
∵g′(x)=f′(x)+1=lnx+2,显然函数g(x)有最小值,故不存在,故②错;
对于③,f(a+x)<f(a)•ex?(a+x)ln(a+x)<alna)•ex?$\frac{(a+x)ln(a+x)}{{e}^{a+x}}<\frac{alna}{{e}^{a}}$,构造函数g(x)=$\frac{xlnx}{{e}^{x}}$,则问题就是要求g(a+x)<g(a)恒成立.
g′(x)=$\frac{lnx-xlnx+1}{{e}^{x}}$,令h(x)=lnx+1-xlnx,则h′(x)=$\frac{1}{x}$-lnx-1,显然h′(x)是减函数.
当x>1时,h′(x)<h′(1)=0,从而函数h(x)在(1,+∞)上也是减函数.
从而当x>3时,h(x)<h(e)=lne+1-elne=2-e<0,即 g′(x)<0,
即函数g(x)=$\frac{xlnx}{{e}^{x}}$在区间(3,+∞)上是减函数.
当a>3时,对于任意的非零正数x,a+x>a>3,进而有g(a+x)<g(a)恒成立,故③正确;
对于④,构造函数h(x)=f(x)f(a)-f′(a)(x-a)=xlnx-xlna-x+a,(x>3)
h′(x)=lnx-lna,可知h(x)在(3,a)递减,在(a,+∞)递减,h(x)≥h(a)=0,∴x≠a时,不等式f(x)>f(a)+f′(a)(x-a)恒成立,故④正确;
故选:C.
点评 本小题主要考查函数与导数的综合应用能力,具体涉及到用导数来研究函数的单调性、极值以及函数零点的情况.属于难题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
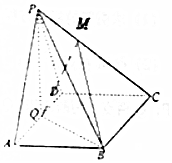 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
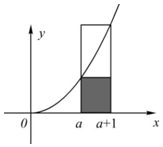 如图所示,由直线x=a,x=a+1(a>0),y=x2及 x 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即 a2<$\int_a^{a+1}{\;}$x2dx<(a+1)2.类比之,若对?n∈N*,不等式$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )
如图所示,由直线x=a,x=a+1(a>0),y=x2及 x 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即 a2<$\int_a^{a+1}{\;}$x2dx<(a+1)2.类比之,若对?n∈N*,不等式$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )| A. | ln$\frac{5}{2}$ | B. | ln 2 | C. | $\frac{1}{2}$ln 2 | D. | $\frac{1}{2}$ln 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
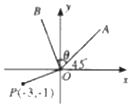 如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )
如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com