练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．如图，是一个算法流程图，当输入的x=5时，那么运行算法流程图输出的结果是（　　）
    A．10B．20C．25D．35

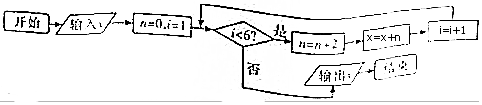
    分析 按照程序框图的流程写出前几次循环的结果，并判断每一次得到的结果是否满足判断框中的条件，直到不满足条件，执行输出即可得解．

    解答 解：模拟程序的运行，可得
    x=5，n=0，i=1
    满足条件i＜6，执行循环体，n=2，x=7，i=2
    满足条件i＜6，执行循环体，n=4，x=11，i=3
    满足条件i＜6，执行循环体，n=6，x=17，i=4
    满足条件i＜6，执行循环体，n=8，x=25，i=5
    满足条件i＜6，执行循环体，n=10，x=35，i=6
    不满足条件i＜6，退出循环，输出x的值为35．
    故选：D．

    点评 本题主要考查程序框图的应用，解决程序框图中的循环结构时；常采用写出前几次循环的结果，找规律，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．已知函数$f（x）={a^x}+\frac{1-t}{a^2}（a＞0，a≠1）$是定义域为R上的奇函数．
    （1）求实数t的值；
    （2）若f（1）＞0，不等式f（x2+bx）+f（4-x）＞0在x∈R上恒成立，求实数b的取值范围；
    （3）若$f（1）=\frac{3}{2}$且$h（x）={a^{2x}}+\frac{1}{{{a^{2x}}}}-2mf（x）$[1，+∞）上最小值为-2，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

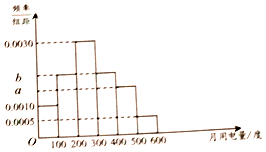    2．某市为了鼓励市民节约用电，实行“阶梯式”电价，将该市每户居民的月用电量划分为三档，月用电量不超过200度的部分按0.5元/度收费，超过200度但不超过400度的部分按0.8元/度收费，超过400度的部分按1.0元/度收费．
    （1）求某户居民用电费用y（单位：元）关于月用电量x（单位：度）的函数解析式；
    （2）为了了解居民的用电情况，通过抽样，获得了今年1月份100户居民每户的用电量，统计分析后得到如图所示的频率分布直方图，若这100户居民中，今年1月份用电费用不超过260元的点80%，求a，b的值；
    （3）在满足（2）的条件下，若以这100户居民用电量的频率代替该月全市居民用户用电量的概率，且同组中的数据用该组区间的中点值代替，记Y为该居民用户1月份的用电费用，求Y的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设复数z满足z+i=i（2-i），则$\overline{z}$=（　　）
    A．1+3iB．-1+3iC．1-iD．-1+i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知函数f（x）=xlnx，x∈（0，+∞），其导函数为f′（x），现有如下命题：
    ①对?x1∈（0，+∞），?x2∈（0，+∞），使得x2f（x1）＞x1f（x2）；
    ②?x1∈（0，+∞），对?x2∈（0，+∞）且x1≠x2，使得f（x1）-f（x2）＜x2-x1；
    ③当a＞3时，对?x∈（0，+∞），不等式f（a+x）＜f（a）•ex恒成立；
    ④当a＞3时，对?x∈（3，+∞），且x≠a时，不等式f（x）＞f（a）+f′（a）（x-a）恒成立；其中真命题的个数为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．某商场在2017年元旦开展“购物折上折”活动，商场内所有商品先按标价打八折，折后价格每满500元再减100元，如某商品标价1500元，则购买该商品的实际付款额为1500×0.8-200=1000元．设购买某商品的实际折扣率=$\frac{实际付款额}{商品的标价}×100%$，某人欲购买标价为2700元的商品，那么他可以享受的实际折扣率约为（　　）
    A．55%B．65%C．75%D．80%

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．如图1，棱形ABCD的边长为6，∠BAD=60°，AC∩BD=O．将棱形ABCD沿对角线AC折起，得到三棱锥B-ACD，点M是棱BC的中点，$DM=3\sqrt{2}$．

    （Ⅰ）求证：OM∥平面ABD；
    （Ⅱ）求三棱锥M-ABD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

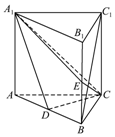    20．如图，直三棱柱ABC-A1B1C1中，D，E分别是AB，BB1的中点，AA1=AC=CB=2，AB=2$\sqrt{2}$．
    （Ⅰ）证明：BC1∥平面A1CD；
    （Ⅱ）求锐二面角D-A1C-E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．如图在直角梯形BB1C1C中，∠CC1B1=90°，BB1∥CC1，CC1=B1C1=2BB1=2，D是CC1的中点．四边形AA1C1C可以通过直角梯形BB1C1C以CC1为轴旋转得到，且二面角B1-CC1-A为120°．
    （1）若点E是线段A1B1上的动点，求证：DE∥平面ABC；
    （2）求二面角B-AC-A1的余弦值．

    查看答案和解析>>

    同步练习册答案