
���� �����������ε��ܳ����a��ֵ����G��x0��y0�������b��c��ֵ���Ӷ������ԲE�ķ��̼��ɣ�
���ֱ����AB��AC��б�ʣ�����ֱ�ߺ�Բ�ķ����飬�ֱ����B��C�����꣬���ֱ��BC�ķ��̣��Ӷ����ֱ�ߺ���Ķ��㼴�ɣ�
��� �⣺�����ɡ�DGF2���ܳ���8���ã�4a=8����ã�a=2��
��|DF1|=3|GF1|��G��DF1���ӳ����ϣ�
��$\overrightarrow{DG}$=$\frac{4}{3}$$\overrightarrow{{DF}_{1}}$����G��x0��y0����
��x0��y0-b��=$\frac{4}{3}$��-c��-b����x0=-$\frac{4}{3}$c��y0=-$\frac{1}{3}$b��
��$\frac{{{x}_{0}}^{2}}{{a}^{2}}$+$\frac{{{y}_{0}}^{2}}{{b}^{2}}$=1����ã�c2=2��
��b2=2����ԲE�ķ�����$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1��
����A��-2��0����ֱ��AB��AC����б�ʣ�
��AB��y=k��x+2����AC��y=-$\frac{1}{k}$��x+2����
��$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\\{y=k��x+2��}\end{array}\right.$�����2k2+1��x2+8k2x+8k2-4=0��
��ã�x1=-2��x2=-$\frac{{4k}^{2}-2}{{2k}^{2}+1}$��
��x2=-$\frac{{4k}^{2}-2}{{2k}^{2}+1}$ʱ��y2=$\frac{4k}{{2k}^{2}+1}$
��B��-$\frac{{4k}^{2}-2}{{2k}^{2}+1}$��$\frac{4k}{{2k}^{2}+1}$����
ͬ��C��$\frac{{2k}^{2}-4}{{k}^{2}+2}$��-$\frac{4k}{{k}^{2}+2}$����
ֱ��BC�ķ�����3kx+2��k2-1��y+2k=0��
ֱ��BC������㣨-$\frac{2}{3}$��0����
���� ���⿼��������Բ�������⣬����ֱ�ߺ���Բ�Ĺ�ϵ�Լ�ת��˼�룬��һ���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30.4��40.2��log0.40.5 | B�� | ${3^{0.4}}��{log_{0.4}}0.5��{4^{0.2}}$ | ||
| C�� | ${log_{0.4}}0.5��{3^{0.4}}��{4^{0.2}}$ | D�� | ${log_{0.4}}0.5��{4^{0.2}}��{3^{0.4}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����������ABC-A1B1C1�У�AB��ƽ��BCC1B1��$��BC{C_1}=\frac{��}{3}��AB=B{B_1}=2��BC=1��D$ΪCC1���е㣮
��ͼ����������ABC-A1B1C1�У�AB��ƽ��BCC1B1��$��BC{C_1}=\frac{��}{3}��AB=B{B_1}=2��BC=1��D$ΪCC1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
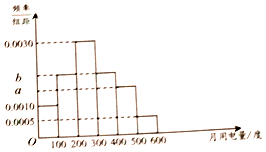 ij��Ϊ�˹��������Լ�õ磬ʵ�С�����ʽ����ۣ�������ÿ����������õ�������Ϊ���������õ���������200�ȵIJ��ְ�0.5Ԫ/���շѣ�����200�ȵ�������400�ȵIJ��ְ�0.8Ԫ/���շѣ�����400�ȵIJ��ְ�1.0Ԫ/���շѣ�
ij��Ϊ�˹��������Լ�õ磬ʵ�С�����ʽ����ۣ�������ÿ����������õ�������Ϊ���������õ���������200�ȵIJ��ְ�0.5Ԫ/���շѣ�����200�ȵ�������400�ȵIJ��ְ�0.8Ԫ/���շѣ�����400�ȵIJ��ְ�1.0Ԫ/���շѣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
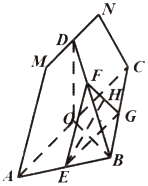 ��ͼ��ʾ���ı���AMNCΪ�������Σ���ABCΪֱ�������Σ�ƽ��AMNC��ƽ��ABC��ֱ��AB=BC��AM=CN����O��D��E�ֱ���AC��MN��AB���е㣮����E��ƽ����ƽ��AMNC�Ľ���ֱ�BD��BC�ڵ�F��G��H��FG���е㣮
��ͼ��ʾ���ı���AMNCΪ�������Σ���ABCΪֱ�������Σ�ƽ��AMNC��ƽ��ABC��ֱ��AB=BC��AM=CN����O��D��E�ֱ���AC��MN��AB���е㣮����E��ƽ����ƽ��AMNC�Ľ���ֱ�BD��BC�ڵ�F��G��H��FG���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com