
| n |
 |
| i=1 |
| 21 |
 |
| n=1 |
| n |
 |
| i=1 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
 |
| i=1 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 21 |
 |
| n=1 |
| 1 |
| 4 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
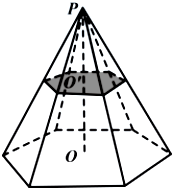 如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
如图,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在水平放置的边长为40cm的正方形轨道模型上,质点甲从A点出发以8cm/s的速度沿点A-B-C方向运动,同时另一质点乙从B点出发以10cm/s的速度沿点B-C-D方向运动.
如图所示,在水平放置的边长为40cm的正方形轨道模型上,质点甲从A点出发以8cm/s的速度沿点A-B-C方向运动,同时另一质点乙从B点出发以10cm/s的速度沿点B-C-D方向运动.查看答案和解析>>
科目:高中数学 来源: 题型:
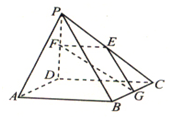 如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.
如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com