练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．一个扇形OAB的面积是1cm2，它的周长是4cm，则弦长AB=（　　）
    A．2B．2sin 1C．2sin 2D．sin 1

    分析 由已知利用扇形面积公式，可求扇形的半径和弧长，过O作OH⊥AB于H，解三角形即可得解AB的值．

    解答 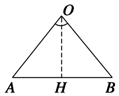解：设扇形的半径为r cm，弧长为l cm，
    则：$\left\{\begin{array}{l}{\frac{1}{2}lr=1}\\{l+2r=4}\end{array}\right.$，解得：$\left\{\begin{array}{l}{r=1}\\{l=2}\end{array}\right.$，
    ∴圆心角α=$\frac{l}{r}$=2．
    如图，过O作OH⊥AB于H，则∠AOH=1 rad．
    ∴AH=1•sin 1=sin 1（cm），
    ∴AB=2sin 1（cm）．
    故选：B．

    点评 本题主要考查了扇形的面积公式，弧长公式，同角三角函数基本关系式的应用，考查了数形结合思想，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．已知a＞0，设函数f（x）=$\frac{201{6}^{x+1}+2011}{201{6}^{x}+1}$+x3（x∈[-a，a]）的最大值为M，最小值为N，则M+N的值为（　　）
    A．2016B．4026C．4027D．4028

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．设函数f（x）=kax-a-x（a＞0且a≠1，k∈R），f（x）是定义域为R的奇函数．
    （1）求k的值
    （2）已知f（1）=$\frac{15}{4}$，函数g（x）=a2x+a-2x-2f（x），x∈[0，1]，求g（x）的值域；
    （3）在第（2）问的条件下，试问是否存在正整数λ，使得f（2x）≥λ•f（x）对任意x∈[-$\frac{1}{2}$，$\frac{1}{2}$]恒成立？若存在，请求出所有的正整数λ；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知点A（m，-3）在抛物线y2=2px（p＞0）上，它到抛物线焦点F的距离为5，求m和p的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知函数f（x）=x2-mlnx在[2，+∞）上单调递增，则实数m的取值范围为（-∞，8]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．函数f（x）=$\frac{1}{3}a{x^3}+\frac{1}{2}a{x^2}$-2ax+2a+1图象经过四个象限的必要而不充分条件是（　　）
    A．-$\frac{4}{3}$＜x＜-$\frac{1}{3}$B．-2＜a＜0C．-$\frac{6}{5}$＜a＜-$\frac{3}{16}$D．-1＜a＜-$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．求下列函数的定义域
    （1）y=$\sqrt{x+3}$+$\frac{1}{x+2}$
    （2）y=$\sqrt{lo{g}_{3}x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数g（x）=x2-ax+b，其图象对称轴为直线x=2，且g（x）的最小值为-1，设f（x）=$\frac{g（x）}{x}$．
    （1）求实数a，b的值；
    （2）若不等式f（3x）-t•3x≥0在x∈[-2，2]上恒成立，求实数t的取值范围；
    （3）若关于x的方程f（|2x-2|）+k•$\frac{2}{|{2}^{x}-2|}$-3k=0有三个不同的实数解，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知θ服从$[{-\frac{π}{2}，\frac{π}{2}}]$上的均匀分布，则2|sinθ|＜$\sqrt{3}$成立的概率为$\frac{2}{3}$．

    查看答案和解析>>

    同步练习册答案