
���� ��1�����ݺ���g��x��=x2-ax+b����ͼ��Գ���Ϊֱ��x=2����g��x������СֵΪ-1���ɵ�ʵ��a��b��ֵ��
��2��������ʽf��3x��-t•3x��0��x��[-2��2]�Ϻ������t��$3•��\frac{1}{{3}^{x}}��^{2}-4��\frac{1}{{3}^{x}}��+1$��x��[-2��2]�Ϻ�����������õ�ʵ��t��ȡֵ��Χ��
��3��������x�ķ���f��|2x-2|��+k•$\frac{2}{|{2}^{x}-2|}$-3k=0��������ͬ��ʵ���⣬��t2-��4+3k��t+��3+2k��=0��������������һ�������䣨0��2���ϣ�һ��������[2��+�ޣ��������ɵ�ʵ��k��ȡֵ��Χ��
��� �⣺��1���ߺ���g��x��=x2-ax+b����ͼ��Գ���Ϊֱ��x=2��
��$\frac{a}{2}$=2��
��ã�a=4��
��x=2ʱ������ȡ��Сֵb-4=-1��
��ã�b=3��
��2���ɣ�1���ã�g��x��=x2-4x+3��
f��x��=x-4+$\frac{3}{x}$
������ʽf��3x��-t•3x��0��x��[-2��2]�Ϻ������
��t��$3•��\frac{1}{{3}^{x}}��^{2}-4��\frac{1}{{3}^{x}}��+1$��x��[-2��2]�Ϻ������
��3x=$\frac{2}{3}$����x=log32-1ʱ��$3•��\frac{1}{{3}^{x}}��^{2}-4��\frac{1}{{3}^{x}}��+1$ȡ��Сֵ-$\frac{1}{3}$��
��t��-$\frac{1}{3}$��
��3����t=|2x-2|��t��0��
��ԭ���̿ɻ�Ϊ��t+$\frac{3}{t}$-4+$\frac{2k}{t}$-3k=0��
��t2-��4+3k��t+��3+2k��=0��
������x�ķ���f��|2x-2|��+k•$\frac{2}{|{2}^{x}-2|}$-3k=0��������ͬ��ʵ���⣬
��t2-��4+3k��t+��3+2k��=0����������
����һ�������䣨0��2���ϣ�һ��������[2��+�ޣ���
��h��t��=t2-��4+3k��t+��3+2k����
��$\left\{\begin{array}{l}����0\\ h��0����0\\ h��2����0\end{array}\right.$��
��$\left\{\begin{array}{l}��4+3k��^{2}-4��3+2k����0\\ 3+2k��0\\ 4-2��4+3k��+��3+2k����0\end{array}\right.$��
��ã�k��[-$\frac{1}{4}$��+�ޣ�
���� ���⿼���֪ʶ���Ƕ��κ�����ͼ������ʣ�������������⣬���̸��ĸ�����ת��˼�룬�Ѷ��е���


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����������ABC-A1B1C1�У�AA1�͵���ABC��AC��BC��AC=BC=$\frac{1}{2}$AA1=2��D��AC���е㣮
��ͼ����������ABC-A1B1C1�У�AA1�͵���ABC��AC��BC��AC=BC=$\frac{1}{2}$AA1=2��D��AC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 2sin 1 | C�� | 2sin 2 | D�� | sin 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��$\frac{2}{a}$��x��1} | B�� | {x|$\frac{2}{a}$��x��1} | C�� | {x|x��1��x��$\frac{2}{a}$} | D�� | {x|1��x��$\frac{2}{a}$} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
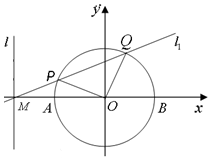 ��ֱ֪��l�ķ���Ϊx=-2����ֱ��l��x�ύ�ڵ�M��ԲO��x2+y2=1��x�ύ��A��B���㣮
��ֱ֪��l�ķ���Ϊx=-2����ֱ��l��x�ύ�ڵ�M��ԲO��x2+y2=1��x�ύ��A��B���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �溯�������ڣ�0��1������������ | B�� | �溯�������ڣ�0��1�����Ǽ����� | ||
| C�� | ż���������ڣ�0��1������������ | D�� | ż���������ڣ�0��1�����Ǽ����� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com