
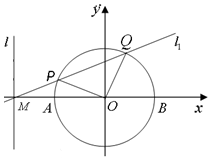
 ��ֱ֪��l�ķ���Ϊx=-2����ֱ��l��x�ύ�ڵ�M��ԲO��x2+y2=1��x�ύ��A��B���㣮
��ֱ֪��l�ķ���Ϊx=-2����ֱ��l��x�ύ�ڵ�M��ԲO��x2+y2=1��x�ύ��A��B���㣮���� ��1����PQΪԲ�ܵ�$\frac{1}{4}$���ɵ�$��POQ=\frac{��}{2}$��O�㵽ֱ��l1�ľ���Ϊ$\frac{{\sqrt{2}}}{2}$������2�֣������õ㵽ֱ�ߵľ��빫ʽ���ɵó���
��2������Բ����Ϊ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$���뽹��Ϊc����$\frac{a^2}{c}=2$��������Բ��Բ�ĶԳ����ʼ��ɵó���
��3�����е�ΪN����������ã���Rt��MON�У�MO=2��ON=1�����NMO=30�㣬N�������Ϊ$��-\frac{1}{2}��\frac{{\sqrt{3}}}{2}��$��������������������㹫ʽ���ɵó���
��� 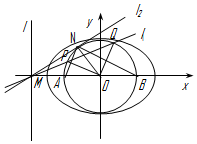 �⣺��1����PQΪԲ�ܵ�$\frac{1}{4}$����$��POQ=\frac{��}{2}$����O�㵽ֱ��l1�ľ���Ϊ$\frac{{\sqrt{2}}}{2}$������2�֣�
�⣺��1����PQΪԲ�ܵ�$\frac{1}{4}$����$��POQ=\frac{��}{2}$����O�㵽ֱ��l1�ľ���Ϊ$\frac{{\sqrt{2}}}{2}$������2�֣�
��l1�ķ���Ϊy=k��x+2������$\frac{|2k|}{{\sqrt{{k^2}+1}}}=\frac{{\sqrt{2}}}{2}$����${k^2}=\frac{1}{7}$����l1�ķ���Ϊ$y=��\frac{{\sqrt{7}}}{7}��x+2��$������5�֣�
��2������Բ����Ϊ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$���뽹��Ϊc����$\frac{a^2}{c}=2$������Բ��ԲOǡ��������ͬ�Ĺ����㣬������Բ��Բ�ĶԳ���
��a=1��b=1������6�֣�
��a=1ʱ��$c=\frac{1}{2}��{b^2}={a^2}-{c^2}=\frac{3}{4}$����������Բ����Ϊ${x^2}+\frac{{4{y^2}}}{3}=1$������8�֣�
��b=1ʱ��b2+c2=2c����c=1����a2=b2+c2=2��
������Բ����Ϊ$\frac{x^2}{2}+{y^2}=1$������10�֣�
��3�����е�ΪN����������ã���Rt��MON�У�MO=2��ON=1�����NMO=30�㣬
N�������Ϊ$��-\frac{1}{2}��\frac{{\sqrt{3}}}{2}��$������11�֣�
����ԲΪ$\frac{x^2}{2}+{y^2}=1$���佹��F1��F2
�ֱ�Ϊ��A��B��${S_{��N{F_1}{F_2}}}=\frac{1}{2}��2��\frac{{\sqrt{3}}}{2}=\frac{{\sqrt{3}}}{2}$������13�֣�
����ԲΪ${x^2}+\frac{{4{y^2}}}{3}=1$���佹��Ϊ${F_1}��-\frac{1}{2}��0����{F_2}��\frac{1}{2}��0��$��
��ʱ${S_{��N{F_1}{F_2}}}=\frac{1}{2}��1��\frac{{\sqrt{3}}}{2}=\frac{{\sqrt{3}}}{4}$����16�֣�
���� ���⿼������Բ��Բ�ı����̼������ʡ�Բ�����ߵ����ʡ�������������㹫ʽ���㵽ֱ�ߵľ��빫ʽ����������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | a��c��b | C�� | c��a��b | D�� | c��b��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com