
分析 (1)由题意可得方程ax2+x-a-b=0的两根分别为-1、3,且a<0,利用韦达定理,可得a,b的值;
(2)若a<0,等式为ax2+x-(a+1)>0,即$(x-1)(x+\frac{a+1}{a})<0$,分类讨论,可得不同情况下不等式的解集.
解答 (本小题满分12分)
解:(1)由题意可得方程ax2+x-a-b=0的两根分别为-1、3,且a<0 …(1分)
∴$\left\{\begin{array}{l}-1+3=-\frac{1}{a}\\-1×3=\frac{-a-b}{a}\end{array}\right.$解得$\left\{\begin{array}{l}a=-\frac{1}{2}\\ b=-1\end{array}\right.$…(4分)
(2)若a<0,不等式为ax2+x-(a+1)>0,即$(x-1)(x+\frac{a+1}{a})<0$…(6分)
∵$1-(-\frac{a+1}{a})=\frac{2a+1}{a}=0⇒a=-\frac{1}{2}$.
∴当$a<-\frac{1}{2}$时,$-\frac{a+1}{a}<1$,不等式的解集为$(-\frac{a+1}{a},1)$; …(8分)
当$a=-\frac{1}{2}$时,$-\frac{a+1}{a}=1$,不等式的解集为∅; …(10分)
当$-\frac{1}{2}<a<0$时,$-\frac{a+1}{a}>1$,不等式的解集为$(1,-\frac{a+1}{a})$…(12分)
(如上,没有“综上所述…”,不扣分,但解集表达不规范每处扣(1分),最多累计扣2分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | {x|x<$\frac{2}{a}$或x>1} | B. | {x|$\frac{2}{a}$<x<1} | C. | {x|x<1或x>$\frac{2}{a}$} | D. | {x|1<x<$\frac{2}{a}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
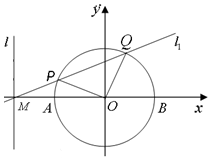 已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点.
已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆心坐标为$(1,\sqrt{3})$的圆M与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x相切于A、B两点,另一圆N1与圆M外切(圆N1在圆M的斜上方),且与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x分别切于C、D两点.(如图)
已知圆心坐标为$(1,\sqrt{3})$的圆M与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x相切于A、B两点,另一圆N1与圆M外切(圆N1在圆M的斜上方),且与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x分别切于C、D两点.(如图)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com