
分析 逐项判断即可.①分别讨论x,y的符号,代入条件等式一判断;②直接代入检验即可;③利用赋值法可得;④举反例即可判断.
解答 解:①若x=3,y=1,则f2(x)-f2(y)=1-1=0,f(x+y)f(x-y)=f(4)f(2)=1,不满足集合条件,故f(x)∉M,故①错误;
②由f(x)=2x得:f2(x)-f2(y)=4x2-4y2,f(x+y)f(x-y)=2(x+y)•2(x-y)=4x2-4y2,满足等式,故f(x)∈M,故②正确;
③由题意知,函数f(x)满足f2(x)-f2(y)=f(x+y)f(x-y),令x=y=0得:f(0)=0;再令x=0得:-f2(y)=f(y)f(-y),即有f(y)[f(y)+f(-y)]=0,所以f(y)=0或f(-y)=-f(y),当f(y)=0时,函数图象关于原点对称,当f(-y)=-f(y)时,函数为奇函数,图象也关于原点对称,故③正确;④取f(x)=-x,因为f2(x)-f2(y)=x2-y2,f(x+y)f(x-y)=-(x+y)(y-x)=x2-y2,所以f(x)∈M,而f(x)=-x为减函数,故④错误.
综上可得:②③正确.
故答案为:②③.
点评 本题是一道创新题,解题关键在于正确理解集合M中元素所满足的关系,考查了分析问题和解决问题的能力.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
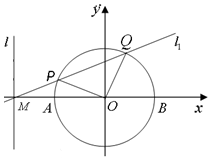 已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点.
已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆心坐标为$(1,\sqrt{3})$的圆M与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x相切于A、B两点,另一圆N1与圆M外切(圆N1在圆M的斜上方),且与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x分别切于C、D两点.(如图)
已知圆心坐标为$(1,\sqrt{3})$的圆M与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x相切于A、B两点,另一圆N1与圆M外切(圆N1在圆M的斜上方),且与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x分别切于C、D两点.(如图)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com