
分析 (1)f(x)是定义域为R的奇函数.f(0)=0,可得k的值.
(2)f(1)=$\frac{15}{4}$,求出a的值,可得f(x),函数g(x)=a2x+a-2x-2f(x),x∈[0,1],可求g(x)的值域;
(3)假设存在满足条件的正整数λ,转化成不等式问题求解,分类讨论其正整数λ的值即可.
解答 解:(1)由题意:函数f(x)=kax-a-x(a>0且a≠1,k∈R),f(x)是定义域为R的奇函数.
∴f(0)=0,即k-1=0,解得:k=1,
故得函数f(x)=ax-a-x,
(2)∵f(1)=$\frac{15}{4}$,
可得f(1)=$a-\frac{1}{a}$=$\frac{15}{4}$,
解得:a=4或a=$-\frac{1}{4}$,
∵a>0,
故得:a=4.
∴函数f(x)=4x-4-x
∵函数g(x)=a2x+a-2x-2f(x),x∈[0,1],
∴g(x)=42x+4-2x-2(4x-4-x)=(4x-4-x)2-2(4x-4-x)+2
令t=4x-4-x,
∵x∈[0,1],由(1)知t=f(x)在[0,1]上为增函数,
∴t∈[0,$\frac{15}{4}$].
那么:g(x)=(4x-4-x)2-2(4x-4-x)+2转化为h(t)=t2-2t+2,
函数h(t)图象开口向上,对称轴t=1,
∴当$t=\frac{15}{4}$时,h(t)有最大值$\frac{137}{16}$;即函数g(x)最大值为$\frac{137}{16}$.
当t=1时,h(t)有最小值1,即函数g(x)最小值为1.
∴函数g(x)的值域为[1,$\frac{137}{16}$].
(3)由(2)可得f(2x)=42x-4-2x=(4x+4-x)(4x-4-x)
∵f(2x)≥λ•f(x),即为(4x+4-x)(4x-4-x)≥λ•(4x-4-x).
假设存在满足条件的正整数λ,
∵x∈[-$\frac{1}{2}$,$\frac{1}{2}$],
①当x=0时,不等式恒成立,
故得:λ∈R.
②当x∈(0,$\frac{1}{2}$]时,4x-4-x>0,不等式转化为4x+4-x≥λ;
令u=4x,
则:1<u≤2.
易证:Z=$u+\frac{1}{u}$在(1,2]上是增函数,其最小值为2.
故得:λ≤2.
③当x∈[-$\frac{1}{2}$,0)时,4x-4-x<0,不等式转化为4x+4-x≤λ;
令v=4x,
则:$\frac{1}{2}$≤v<1,
易证:Z′=$v+\frac{1}{v}$在[$\frac{1}{2}$,1)上是减函数,其最大值为$\frac{5}{2}$.
故得:λ≥$\frac{5}{2}$.
综上所得,λ不存在固定的值.
∴不存在正整数λ,使得f(2x)≥λ•f(x)对任意x∈[-$\frac{1}{2}$,$\frac{1}{2}$]恒成立.
点评 本题考查指数函数的解析式的求法,值域的综合问题,恒成立的讨论转化为不等式求解.属于难题.


科目:高中数学 来源: 题型:选择题
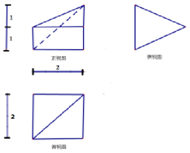
| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=2,D是AC的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=2,D是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com