练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知函数f（x）在R上可导，且f（x）=2x+f'（0）•（x2-1），则f（0）的值为（　　）
    A．ln2B．0C．1D．1-ln2

    分析 利用求导法则求出f′（x）的值，令x=0求出f′（0）的值，即可确定出f（0）的值．

    解答 解：根据题意得：f′（x）=2xln2-f′（0）•2x，
    令x=0，得到f′（0）=ln2，
    则f（0）=20+f'（0）•（02-1）=1-ln2
    故选：D．

    点评 此题考查了导数的运算，熟练掌握求导法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．下面的图形无限向内延续，最外面的正方形的边长是1，从外到内，第n个正方形与其内切圆之间的深色图形面积记为${S_n}（n∈{N^*}）$．
    （1）试写出Sn+1与${S_n}（n∈{N^*}）$的递推关系式；
    （2）设${T_n}={S_1}+{S_2}+…+{S_n}（n∈{N^*}）$，求Tn的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．下列说法正确的是（　　）
    A．类比推理、归纳推理、演绎推理都是合情推理
    B．合情推理得到的结论一定是正确的
    C．合情推理得到的结论不一定正确
    D．归纳推理得到的结论一定是正确的

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．下列有关于f（x）=ln（1+|x|）-$\frac{1}{1{+x}^{2}}$的性质的描述，正确的是（　　）
    A．奇函数，在R上单调递增
    B．奇函数，在（-∞，0）上单调递增，在（0，+∞）上单调递增
    C．偶函数，在（-∞，0）上单调递减，在（0，+∞）上单调递增
    D．偶函数，在（-∞，0）上单调递增，在（0，+∞）上单调递减

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知向量$\vec a，\vec b，\vec c$是空间的一个单位正交基底，向量$\vec a+\vec b，\vec a-\vec b，\vec c$是空间的另一个基底．若向量$\vec m$在基底$\vec a，\vec b，\vec c$下的坐标为（1，2，3），则$\vec m$在基底$\vec a+\vec b，\vec a-\vec b，\vec c$下的坐标为（$\frac{3}{2}$，-$\frac{1}{2}$，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若函数$f（x）=\frac{e^x}{x}$在x=a处有极小值，则实数a等于1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=$\frac{1}{3}{x^3}-{x^2}+（{1-{m^2}}）x（{0＜m＜1}）$
    （1）求函数f（x）的极大值点和极小值点；
    （2）若f（x）恰好有三个零点，求实数m取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知中心在原点，焦点在x轴上的椭圆的一个顶点坐标为（0，1），其离心率为$\frac{\sqrt{6}}{3}$
    （1）求椭圆的标准方程；
    （2）椭圆上一点P满足∠F1PF2=60°，其中F1，F2为椭圆的左右焦点，求△F1PF2的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

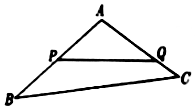    19．如图，某生态园将一块三角形地ABC的一角APQ开辟为水果园，已知角A为120°，AB，AC的长度均大于200米，现在边界AP，AQ处建围墙，在PQ处围竹篱笆．
    （1）若围墙AP、AQ总长度为200米，如何可使得三角形地块APQ面积最大？
    （2）已知竹篱笆长为50$\sqrt{3}$米，AP段围墙高1米，AQ段围墙高2米，造价均为每平方米100元，若AP≥AQ，求围墙总造价的取值范围．

    查看答案和解析>>

    同步练习册答案