Question

1．已知函数f（x）=$\frac{1}{3}{x^3}-{x^2}+（{1-{m^2}}）x（{0＜m＜1}）$
（1）求函数f（x）的极大值点和极小值点；
（2）若f（x）恰好有三个零点，求实数m取值范围．

Answer 1

分析 （1）求出函数的导数，解关于导函数的不等式，求出函数的单调区间，从而求出函数的极值点；
（2）问题转化为关于m的不等式组，解出即可．

解答 解：（1）令f'（x）=x²-2x+1-m²=0，得x₁=1-m；x₂=1+m，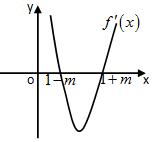
，
x，f′（x），f（x）的变化如下：

x	（-∞，1-m）	（1-m，1+m）	（1+m，+∞）
f'（x）	+	-	+
f（x）	递增	递减	递增

f（x）在（-∞，1-m）和（1+m，+∞）上为增函数；在（1-m，1+m）上为减函数，
函数f（x）的极大值点为x=1-m，极小值点为x=1+m；
（2）若f（x）恰好有三个零点，
则$\left\{{\begin{array}{l}{f（{1-m}）＞0}\\{f（{1+m}）＜0}\end{array}}\right.$，又0＜m＜1，得：$\frac{1}{2}＜m＜1$．

点评 本题考查了函数的单调性、极值点问题，考查导数的应用以及函数的零点问题，是一道中档题．