
| A�� | ������y=$\frac{1}{4}$x2�Ľ�������Ϊ��0��1�� | |
| B�� | ˫����$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=2���Ҷ��㵽�����ҽ���ľ���֮��Ϊ3 | |
| C�� | ����f��x��=x3-3x2+b�����䣨-�ޣ�-1������ֵ�� | |
| D�� | ����f��x��=x3-3x2+5�ڵ㣨1��f��1���������ߵ���б�Ǵ���$\frac{3��}{4}$ |
���� �������֪����p�Ǽ����⣬���ݸ���������жϣ����q�Ǽ����⣬Ȼ����һ�ж��ĸ�ѡ��ô𰸣�
��� �⣺����p��?x��R��3x-3��0���Ǽ����⣬
�ʩVp�������⣬
�����Vp����q�Ǽ����⣬
��q�Ǽ����⣬
����A��������y=$\frac{1}{4}$x2��Ϊx2=4y���佹������Ϊ��0��1������A�������⣻
����B��˫����$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=2���Ҷ���Ϊ��$\sqrt{2}$��0�������ҽ���ֱ�ΪF1��$-2\sqrt{2}$��0����F2��$2\sqrt{2}$��0����
�Ҷ��㵽�����ҽ���ľ���֮��Ϊ$\frac{\sqrt{2}-��-2\sqrt{2}��}{2\sqrt{2}-\sqrt{2}}=3$����BΪ�����⣻
����C������f��x��=x3-3x2+b��f�䣨x��=3x2-6x����f�䣨x��=3x2-6x=0����x=0��x=2��
��x�ʣ�-�ޣ�0������2��+�ޣ�ʱ��f��x��Ϊ����������x�ʣ�0��2��ʱ��f��x��Ϊ������������f��x��=x3-3x2+b�����䣨-�ޣ�-1������ֵ�㣬��CΪ�����⣻
����D����f��x��=x3-3x2+5����f�䣨x��=3x2-6x����f�䣨1��=-3��-1��������f��x��=x3-3x2+5�ڵ㣨1��f��1���������ߵ���б��С��$\frac{3��}{4}$����D�Ǽ����⣮
��ѡ��D��
���� ���⿼�����������ж���Ӧ�ã�������˫���ߵļ������ʣ��������õ����о������ĵ����ԣ����е��⣮


 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
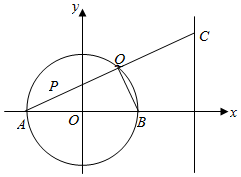 ��֪ԲO��x2+y2=9��ֱ��l1��x=6��ԲO��x���ཻ�ڵ�A��B����ͼ������P��-1��2����ԲO��һ�㣬��QΪԲO����һ�㣨���ڵ�A��B����ֱ��AQ��l1�ཻ�ڵ�C��
��֪ԲO��x2+y2=9��ֱ��l1��x=6��ԲO��x���ཻ�ڵ�A��B����ͼ������P��-1��2����ԲO��һ�㣬��QΪԲO����һ�㣨���ڵ�A��B����ֱ��AQ��l1�ཻ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
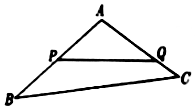 ��ͼ��ij��̬��һ�������ε�ABC��һ��APQ����Ϊˮ������֪��AΪ120�㣬AB��AC�ij��Ⱦ�����200�ף����ڱ߽�AP��AQ����Χǽ����PQ��Χ����ʣ�
��ͼ��ij��̬��һ�������ε�ABC��һ��APQ����Ϊˮ������֪��AΪ120�㣬AB��AC�ij��Ⱦ�����200�ף����ڱ߽�AP��AQ����Χǽ����PQ��Χ����ʣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
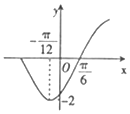 �躯��f��x��=cos2x-$\sqrt{3}$sin2x����y=f��x����ͼ������ƽ��$�գ�{|��|��\frac{��}{2}}��$����λ�õ��IJ���ͼ����ͼ��ʾ����f���գ���ֵ���ڣ�������
�躯��f��x��=cos2x-$\sqrt{3}$sin2x����y=f��x����ͼ������ƽ��$�գ�{|��|��\frac{��}{2}}��$����λ�õ��IJ���ͼ����ͼ��ʾ����f���գ���ֵ���ڣ�������| A�� | $-\sqrt{3}$ | B�� | $\sqrt{3}$ | C�� | -1 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x1��x2 | B�� | x1��x2 | C�� | ${x}_{1}^{2}$��${x}_{2}^{2}$ | D�� | x1+x2=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}+i$ | B�� | $\sqrt{2}-i$ | C�� | $1+\sqrt{2}i$ | D�� | $1-\sqrt{2}i$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com