练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知Sn=na1+
    n(n-1)
    2
    d    ，求证：{an}是等差数列．
    考点：等差关系的确定
    专题：等差数列与等比数列
    分析：当n=1时，a1=S1=a1．当n≥2时，an=Sn-Sn-1=a1+（n-1）d，只要证明an-an-1=常数即可．，
    解答： 证明：当n=1时，a1=S1=a1．
    当n≥2时，an=Sn-Sn-1=na1+
    n(n-1)
    2
    d    -[(n-1)a1+
    (n-1)(n-2)
    2
    d]
    =a1+（n-1）d，
    ∴an-an-1=d，
    ∴数列{an}是等差数列．
    点评：本题考查了等差数列的定义通项公式及其前n项和公式，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

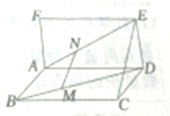    如图所示，已知矩形ABCD和矩形ADEF所在的平面相互垂直，点MN分别在对角线BDAE上，且BM=
    1
    3
    BD，AN=
    1
    3
    AE，求证：向量
    MN
    ，
    CD
    ，
    DE
    共面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若A={x|3x-7＞0}，则∁RA=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知，若a，b在区间（0，π），且sina+sinb=sina•sinb，求cos（a-b）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求函数y=
    3x
    9x+1
    +2的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

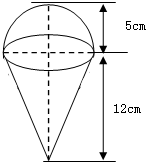    如图，一个圆锥形的空杯子上面放着一个半球形的冰淇淋，假设冰淇淋融化后体积不变，是否会溢出杯子？请说明理由．请用你的计算数据说明理由．（冰、水的体积差异忽略不计）（π取3.14）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设向量
    a
    =（sinx-1，1），
    b
    =（sinx+3，1），
    c
    =（-1，-2），
    d
    =（k，1），k∈R．
    （Ⅰ）若x∈[-
    π
    2
    ，
    π
    2
    ]，且
    a
    ∥（
    b
    +
    c
    ），求x的值；
    （Ⅱ）若存在x∈R，使得（
    a
    +
    d
    ）⊥（
    b
    +
    c
    ），求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知在正方体ABCD-A1B1C1D1中，面对角线A1B、BC1的中点为E、F，求证：EF∥平面ABCD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （Ⅰ） 如图，一个扇形OAB的面积是1cm2，它的周长是4cm，求圆心角的弧度数和弦长AB．
    （Ⅱ） 已知f（x）=-sin2x+sinx+a，若1≤f（x）≤
    17
    4
    对一切x∈R恒成立，求实数a的范围．

    查看答案和解析>>

    同步练习册答案