
分析 (I)求函数f(x)的解析式;
(II)化简不等式f(x)<$\frac{(k+1)x-k}{2-x}$.通过k 的值的讨论,利用不等式的解法求解即可.
解答 解:(I)把x1=3,x2=(4分)别代入方程$\frac{{x}^{2}}{ax+b}$-x+12=0,
得$\left\{\begin{array}{l}\frac{9}{3a+b}=-9\\ \frac{16}{4a+b}=-8\end{array}$解得$\left\{\begin{array}{l}a=-1\\ b=2\end{array}$,
所以f(x)=$\frac{{x}^{2}}{-x+2}$(x≠2);
(II)不等式即为$\frac{{x}^{2}}{-x+2}$<$\frac{(k+1)x-k}{2-x}$.可化为$\frac{{x}^{2}-(k+1)x+k}{2-x}$<0,
即(x-2)(x-1)(x-k)>0,
当k=2时,不等式为(x-2)2(x-1)>0解集为(1,2 )∪(2,+∞),
当k>2 时,由穿根法解得解集为(1,2 )∪(k,+∞).
点评 本题考查函数与方程的应用,函数的零点判定定理的应用,不等式的解法,考查计算能力.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y-1=0 | B. | x-2y+1=0 | C. | 2x+y-2=0 | D. | x+2y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
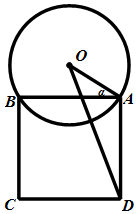 某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)
某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点.
在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com