Question

20．在正方体ABCD-A₁B₁C₁D₁中，M、N、P分别是AD₁、BD和B₁C的中点．
（1）求证：平面MNP∥平面CC₁D₁D．
（2）求二面角N-B₁C-B的正切值．

Answer 1

分析 （1）连接AC，CD₁，连接BC₁，C₁D，利用三角形中位线定理可得MN∥平面CC₁D₁D．PN∥平面CC₁D₁D，再由面面平行的判定可得平面MNP∥平面CC₁D₁D；
（2）取BC的中点R，过R做B₁C的垂线，垂足为E，连接NE，NR，可证∠NER为二面角N-B₁C-B的平面角，设正方体的棱长为2，则NR=1，RE=$\frac{1}{4}B{C}_{1}=\frac{\sqrt{2}}{2}$，求解直角三角形可得二面角N-B₁C-B的正切值．

解答 （1）证明：连接AC，CD₁，连接BC₁，C₁D，
∵ABCD为正方形，N为BD中点，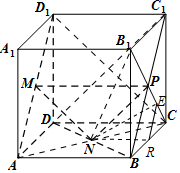
∴N为AC中点，
又∵M为AD₁中点，∴MN∥CD₁，
∵MN?平面CC₁D₁D，CD₁?平面CC₁D₁D，
∴MN∥平面CC₁D₁D．
又∵BB₁CC₁为正方形，P为B₁C中点，
∴P为BC₁中点，
又∵N为BD中点，∴PN∥C₁D．
∵PN?平面CC₁D₁D，C₁D?平面CC₁D₁D，
∴PN∥平面CC₁D₁D，
又∵MN∩PN=N，
∴平面MNP∥平面CC₁D₁D；
（2）解：取BC的中点R，过R做B₁C的垂线，垂足为E，连接NE，NR，
则由NR⊥平面BCC₁B₁，可得NR⊥B₁C，
又RE⊥B₁C，且NR∩RE=R，
∴B₁C⊥平面NRE，则NE⊥B₁C，
则∠NER为二面角N-B₁C-B的平面角，
设正方体的棱长为2，则NR=1，RE=$\frac{1}{4}B{C}_{1}=\frac{\sqrt{2}}{2}$．
在Rt△NRE中，
$tan∠NER=\frac{NR}{ER}=\sqrt{2}$．

点评 本题考查平面与平面平行的判定，考查空间想象能力和思维能力，训练了二面角的平面角的求法，是中档题．