
| A. | [-2,-1] | B. | (-1,3) | C. | (-2,-1) | D. | [-1,2] |
分析 命题p:?x0∈R,x02+(a-1)x0+1<0,可得△=(a-1)2-4>0,解得a范围,命题q:?x∈R,x2+ax+1≥0,△=a2-4≤0,解得a范围.由p∨(¬q)为假命题,可得p为假命题,q为真命题.即可得出.
解答 解:命题p:?x0∈R,x02+(a-1)x0+1<0,则△=(a-1)2-4>0,解得a>3或a<-1.
命题q:?x∈R,x2+ax+1≥0,△=a2-4≤0,解得-2≤a≤2.
∵p∨(¬q)为假命题,
∴p为假命题,q为真命题.
∴$\left\{\begin{array}{l}{-1≤a≤3}\\{-2≤a≤2}\end{array}\right.$,解得-1≤a≤2
则实数a的取值范围是[-1,2].
故选:D.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y-1=0 | B. | x-2y+1=0 | C. | 2x+y-2=0 | D. | x+2y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
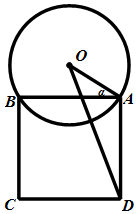 某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)
某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点.
在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$+1 | C. | $\sqrt{3}$-1 | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com