
(本小题满分12分)
已知函数 其中
其中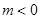
(1)、若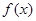 的单调增区间是(0.1),求m的值
的单调增区间是(0.1),求m的值
(2)、当
 时,函数
时,函数 的图像上任意一点的切线斜率恒大于3m,求m的取值范围.
的图像上任意一点的切线斜率恒大于3m,求m的取值范围.
科目:高中数学 来源: 题型:解答题
(本题满分12分)生物体死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.
(Ⅰ)设生物体死亡时体内每克组织中的碳14的含量为1,根据上述规律,写出生物体内碳14的含量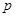 与死亡年数
与死亡年数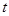 之间的函数关系式;
之间的函数关系式;
(Ⅱ)湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7℅,试推算马王堆汉墓的年代.(精确到个位;辅助数据: )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
设函数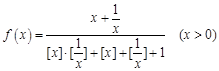 ,其中
,其中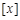 表示不超过
表示不超过 的最大整数,如
的最大整数,如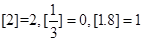 .
.
(1)求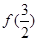 的值;
的值;
(2)若在区间 上存在x,使得
上存在x,使得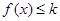 成立,求实数k的取值范围;
成立,求实数k的取值范围;
(3)求函数 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com