
函数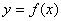 的定义域为
的定义域为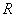 ,若存在常数
,若存在常数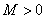 ,使得
,使得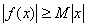 对一切实数
对一切实数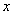 均成立,则称
均成立,则称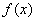 为“圆锥托底型”函数.
为“圆锥托底型”函数.
(1)判断函数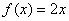 ,
, 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.
(2)若 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出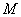 的最大值.
的最大值.
(3)问实数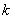 、
、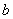 满足什么条件,
满足什么条件,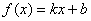 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.
科目:高中数学 来源: 题型:
已知曲线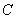 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为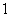 的直线和曲线
的直线和曲线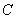 相交,另一个交点记为
相交,另一个交点记为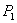 ,过
,过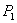 作斜率为
作斜率为 的直线与曲线
的直线与曲线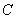 相交,另一个交点记为
相交,另一个交点记为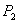 ,过
,过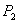 作斜率为
作斜率为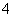 的直线与曲线
的直线与曲线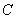 相交,另一个交点记为
相交,另一个交点记为 ,……,如此下去,一般地,过点
,……,如此下去,一般地,过点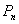 作斜率为
作斜率为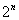 的直线与曲线
的直线与曲线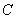 相交,另一个交点记为
相交,另一个交点记为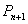 ,设点
,设点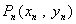 (
(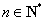 ).
).
(1)指出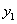 ,并求
,并求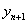 与
与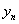 的关系式(
的关系式(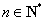 );
);
(2)求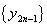 (
(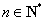 )的通项公式,并指出点列
)的通项公式,并指出点列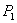 ,
, ,…,
,…,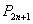 ,… 向哪一点无限接近?说明理由;
,… 向哪一点无限接近?说明理由;
(3)令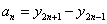 ,数列
,数列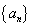 的前
的前 项和为
项和为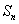 ,设
,设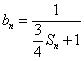 ,求所有可能的乘积
,求所有可能的乘积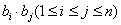 的和.
的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)= 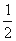
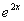 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性;
(2)若a=1,函数g(x)=(x-m)f(x)-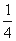
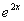 +x2+x在区间(0,+
+x2+x在区间(0,+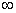 )上为增函数,求整数m 的最大值.
)上为增函数,求整数m 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数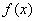 的定义域为
的定义域为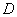 ,若存在闭区间
,若存在闭区间 ,使得函数
,使得函数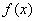 满足:①
满足:①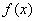 在
在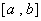 上是单调函数;②
上是单调函数;②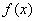 在
在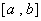 上的值域是
上的值域是 ,则称区间
,则称区间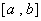 是函数
是函数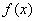 的“和谐区间”.下列结论错误的是……………………………………( )
的“和谐区间”.下列结论错误的是……………………………………( )
A.函数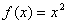 (
(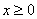 )存在“和谐区间”
)存在“和谐区间”
B.函数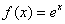 (
(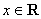 )不存在“和谐区间”
)不存在“和谐区间”
C.函数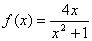
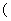
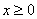 )存在“和谐区间”
)存在“和谐区间”
D.函数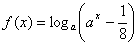 (
(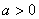 ,
,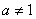 )不存在“和谐区间”
)不存在“和谐区间”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com