
已知曲线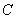 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为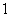 的直线和曲线
的直线和曲线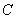 相交,另一个交点记为
相交,另一个交点记为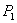 ,过
,过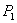 作斜率为
作斜率为 的直线与曲线
的直线与曲线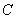 相交,另一个交点记为
相交,另一个交点记为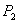 ,过
,过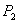 作斜率为
作斜率为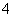 的直线与曲线
的直线与曲线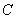 相交,另一个交点记为
相交,另一个交点记为 ,……,如此下去,一般地,过点
,……,如此下去,一般地,过点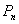 作斜率为
作斜率为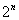 的直线与曲线
的直线与曲线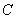 相交,另一个交点记为
相交,另一个交点记为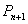 ,设点
,设点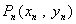 (
(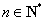 ).
).
(1)指出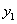 ,并求
,并求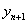 与
与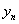 的关系式(
的关系式(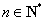 );
);
(2)求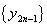 (
(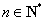 )的通项公式,并指出点列
)的通项公式,并指出点列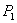 ,
, ,…,
,…,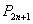 ,… 向哪一点无限接近?说明理由;
,… 向哪一点无限接近?说明理由;
(3)令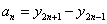 ,数列
,数列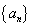 的前
的前 项和为
项和为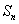 ,设
,设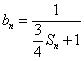 ,求所有可能的乘积
,求所有可能的乘积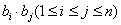 的和.
的和.
科目:高中数学 来源: 题型:
某中学有4位学生申请A,B,C三所大学的自主招生.若每位学生只能申请其中一所大学,且申请其中任何一所大学是等可能的.
(1)求恰有2人申请A大学的概率;
(2)求被申请大学的个数X的概率分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面几何中有如下结论:若正三角形ABC的内切圆面积为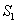 ,外接圆面积为
,外接圆面积为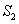 ,则
,则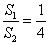 .推广到空间几何体中可以得到类似结论:若正四面体ABCD的内切球体积为
.推广到空间几何体中可以得到类似结论:若正四面体ABCD的内切球体积为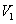 ,外接球体积为
,外接球体积为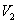 ,则
,则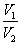 =___________.
=___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二次函数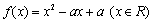 同时满足:①不等式
同时满足:①不等式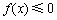 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在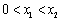 ,使得不等式
,使得不等式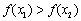 成立.设数列
成立.设数列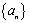 的前
的前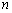 项和为
项和为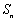 ,且
,且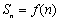 .规定:各项均不为零的数列
.规定:各项均不为零的数列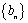 中,所有满足
中,所有满足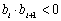 的正整数
的正整数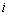 的个数称为这个数列
的个数称为这个数列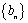 的变号数.若令
的变号数.若令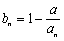 (
(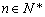 ),则数列
),则数列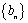 的变号数等于 .
的变号数等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列 ,
, ,
, ,已知
,已知 ,
, ,
, ,
, ,
, ,
, (
( ).
).
(1)求数列 的通项公式;
的通项公式;
(2)求证:对任意 ,
, 为定值;
为定值;
(3)设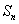 为数列
为数列 的前
的前 项和,若对任意
项和,若对任意 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列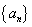 中,
中,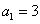 ,
,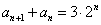 ,
, .
.
(1)证明数列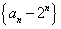 是等比数列,并求数列
是等比数列,并求数列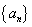 的通项公式;
的通项公式;
(2)在数列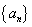 中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(3)若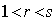 且
且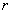 ,
,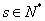 ,求证:使得
,求证:使得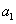 ,
,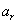 ,
, 成等差数列的点列
成等差数列的点列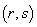 在某一直线上.
在某一直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
函数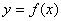 的定义域为
的定义域为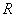 ,若存在常数
,若存在常数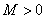 ,使得
,使得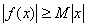 对一切实数
对一切实数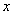 均成立,则称
均成立,则称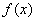 为“圆锥托底型”函数.
为“圆锥托底型”函数.
(1)判断函数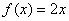 ,
, 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.
(2)若 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出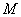 的最大值.
的最大值.
(3)问实数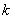 、
、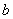 满足什么条件,
满足什么条件,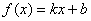 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com