
【题目】已知函数f(x)=ex(其中e为自然对数的底数),g(x)=![]() x+m(m,n∈R).
x+m(m,n∈R).
(1)若T(x)=f(x)g(x),m=1﹣![]() ,求T(x)在[0,1]上的最大值;
,求T(x)在[0,1]上的最大值;
(2)若m=﹣![]() ,n∈N*,求使f(x)的图象恒在g(x)图象上方的最大正整数n.[注意:7<e2<
,n∈N*,求使f(x)的图象恒在g(x)图象上方的最大正整数n.[注意:7<e2<![]() ].
].
【答案】(1)当![]() 时最大值为
时最大值为![]() ;当
;当![]() 时最大值为
时最大值为![]() (2)14
(2)14
【解析】试题分析:
(1)首先求得函数的解析式,然后利用导函数研究函数的最值可得当![]() 时最大值为
时最大值为![]() ;当
;当![]() 时最大值为
时最大值为![]() ;
;
(2)将问题转化为![]() 恒成立,讨论可得最大正整数n为14.
恒成立,讨论可得最大正整数n为14.
试题解析:
解:(1)T(x)=f(x)g(x)
=ex(![]() x+m)=ex(
x+m)=ex(![]() x+1﹣
x+1﹣![]() );
);
故T′(x)=ex(![]() x+1);
x+1);
则当n≥﹣2时,T′(x)≥0;
故T(x)在[0,1]上的最大值为T(1)=e;
当n<﹣2时,x∈[0,﹣![]() )时,T′(x)>0;x∈(﹣
)时,T′(x)>0;x∈(﹣![]() ,1]时,T′(x)<0;
,1]时,T′(x)<0;
T(x)在[0,1]上的最大值为T(﹣![]() )=﹣
)=﹣![]()
![]() ;
;
(2)由题意,f(x)=ex,g(x)=![]() x﹣
x﹣![]() ;
;
故f(x)的图象恒在g(x)图象上方可化为
F(x)=f(x)﹣g(x)=ex﹣![]() x+
x+![]() >0恒成立;F′(x)=ex﹣
>0恒成立;F′(x)=ex﹣![]() ;
;
故F(x)在(﹣∞,ln![]() )上是减函数,在(ln
)上是减函数,在(ln![]() ,+∞)上是增函数;
,+∞)上是增函数;
故可化为F(ln![]() )>0;即
)>0;即![]() (1﹣ln
(1﹣ln![]() )+
)+![]() >0;
>0;
令G(n)=![]() (1﹣ln
(1﹣ln![]() )+
)+![]() ;故G′(n)=﹣
;故G′(n)=﹣![]() (ln
(ln![]() +1)<0;
+1)<0;
故G(n)=![]() (1﹣ln
(1﹣ln![]() )+
)+![]() 是[1,+∞)上的减函数,
是[1,+∞)上的减函数,
而G(2e2)=﹣e2+![]() >0;G(14)=7(1﹣ln7)+
>0;G(14)=7(1﹣ln7)+![]() >0;
>0;
G(15)=7.5(1﹣ln7.5)+![]() <0;故最大正整数n为14.
<0;故最大正整数n为14.


科目:高中数学 来源: 题型:
【题目】某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为[80,90)、[90,100)、[100,110)、[110,120)、[120,130),由此得到两个班测试成绩的频率分布直方图: 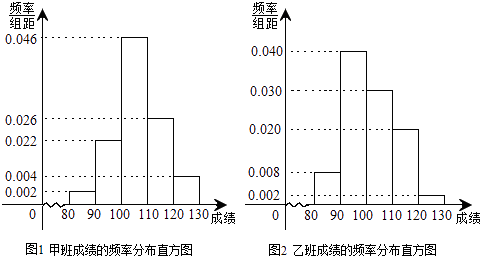
(1)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
成绩小于100分 | 成绩不小于100分 | 合计 | |
甲班 | a= | b= | 50 |
乙班 | c=24 | d=26 | 50 |
合计 | e= | f= | 100 |
(2)现从乙班50人中任意抽取3人,记ξ表示抽到测试成绩在[100,120)的人数,求ξ的分布列和数学期望Eξ.
附:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.204 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选择意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果整理成条形图如下.
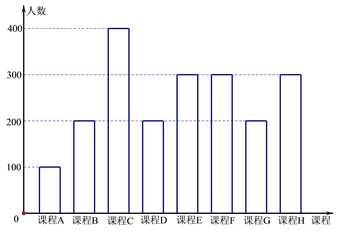
上图中,已知课程![]() 为人文类课程,课程
为人文类课程,课程![]() 为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取
为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取![]() 的学生作为研究样本组(以下简称“组M”).
的学生作为研究样本组(以下简称“组M”).
(Ⅰ)在“组M”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)为参加某地举办的自然科学营活动,从“组M”所有选择自然科学类课程的同学中随机抽取4名同学前往,其中选择课程F或课程H的同学参加本次活动,费用为每人1500元,选择课程G的同学参加,费用为每人2000元.
(ⅰ)设随机变量![]() 表示选出的4名同学中选择课程
表示选出的4名同学中选择课程![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列;
的分布列;
(ⅱ)设随机变量![]() 表示选出的4名同学参加科学营的费用总和,求随机变量
表示选出的4名同学参加科学营的费用总和,求随机变量![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x2﹣mlnx,g(x)=x2﹣(m+1)x,m>0.
x2﹣mlnx,g(x)=x2﹣(m+1)x,m>0.
(1)求函数f(x)的单调区间;
(2)当m≥1时,讨论函数f(x)与g(x)图象的交点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的极坐标方程为ρsin(θ+ ![]() )=
)= ![]() .
.
(1)在极坐标系下写出θ=0和θ= ![]() 时该直线上的两点的极坐标,并画出该直线;
时该直线上的两点的极坐标,并画出该直线;
(2)已知Q是曲线ρ=1上的任意一点,求点Q到直线l的最短距离及此时Q的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,若圆x2+y2=a2被直线x﹣y﹣
,若圆x2+y2=a2被直线x﹣y﹣![]() =0截得的弦长为2
=0截得的弦长为2
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点A、B为动直线y=k(x﹣1),k≠0与椭圆C的两个交点,问:在x轴上是否存在定点M,使得![]() 为定值?若存在,试求出点M的坐标和定值;若不存在,请说明理由.
为定值?若存在,试求出点M的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,设ai=2m(i∈N* , 3m﹣2≤i<3m+1,m∈N*),Si=ai+ai+3+ai+6+ai+9+ai+12 , 则满足Si∈[1000,3000]的i的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,四边形
,四边形![]() 与四边形
与四边形![]() 的面积之和为4.
的面积之和为4.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() (其中
(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 被以线段
被以线段![]() 为直径的圆截得的弦长.
为直径的圆截得的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com