
分析 先求出关于x,y不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥x}\\{x+y≤2}\end{array}\right.$表示的平面区域,再判断不等式2x-y≥k表示的平面区域,通过图象分析直线2x-y-k=0位置在何处时,关于x,y的不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥x}\\{x+y≤2}\\{2x-y≥k}\end{array}\right.$表示的平面区域为三角形,就可求出k的范围.
解答 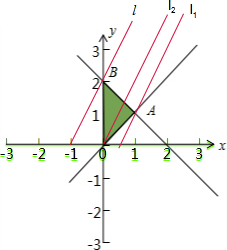 解:关于x,y不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥x}\\{x+y≤2}\end{array}\right.$表示的平面区域为如图三角形ABO:
解:关于x,y不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥x}\\{x+y≤2}\end{array}\right.$表示的平面区域为如图三角形ABO:
可知A(1,21),B(2,0)
而不等式2x-y≥k表示直线2x-y-k=0的左下方,
直线2x-y-k=0与y轴交点坐标为(0,-k),
若直线2x-y-k=0与y轴交点在线段OB上(不包括B点,不包括O点),直线2x-y-k=0在l的左上方,或夹在l1与l2之间.
或直线2x-y-k=0与直线x+y=2的交点在AB内,
关于x,y的不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥x}\\{x+y≤2}\\{2x-y≥k}\end{array}\right.$所表示的平面区域D不为三角形区域.
-k≥2,0≤-k≤2-1,解得:k≤-2或-1≤k≤0.
故答案为:k≤-2或-1≤k≤0.
点评 本题主要考查不等式组表示的平面区域的,是每个不等式表示的平面区域的公共部分.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2x-3y+3=0 | B. | 2x-3y-3=0 | C. | 2x+3y+3=0 | D. | 2x+3y-3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | {-3,-1} | C. | {-3,-1,0} | D. | {0,2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
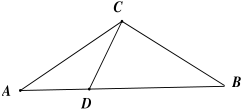 如图,在等腰△ABC中,∠C=120°,DA=DC,过顶点C在∠ACB内部作一条射线CM,与线段AB交于点M,则AM<$\frac{{\sqrt{3}}}{3}$AC的概率为( )
如图,在等腰△ABC中,∠C=120°,DA=DC,过顶点C在∠ACB内部作一条射线CM,与线段AB交于点M,则AM<$\frac{{\sqrt{3}}}{3}$AC的概率为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com