
【题目】已知在多面体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 且平面
且平面![]() 平面
平面![]() .
.
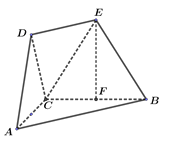
(1)设点![]() 为线段
为线段![]() 的中点,试证明
的中点,试证明![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析(2)![]()
【解析】
(1)由四边形![]() 为平行四边形.∴
为平行四边形.∴![]() ,再结合
,再结合![]() 平面
平面![]() ,即可证明
,即可证明![]() 平面
平面![]() ;
;
(2)由空间向量的应用,建立以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 与
与![]() 平行的直线为
平行的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴的空间直角坐标系,再求出平面
轴的空间直角坐标系,再求出平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,再利用向量夹角公式求解即可.
,再利用向量夹角公式求解即可.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
∵在![]() 中
中![]() ,∴
,∴![]() .
.
∴由平面![]() 平面
平面![]() ,且交线为
,且交线为![]() 得
得![]() 平面
平面![]() .
.
∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,∴
的中点,∴![]() ,且
,且![]() .
.
又![]() ,
,![]() ,∴
,∴![]() ,且
,且![]() .
.
∴四边形![]() 为平行四边形.∴
为平行四边形.∴![]() ,
,
∴![]() 平面
平面![]() .
.
(2)∵![]() 平面
平面![]() ,
,![]() ,
,
∴以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 与
与![]() 平行的直线为
平行的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系.则
轴,建立空间直角坐标系.则![]() ,
,![]() ,
,![]() .
.
∵![]() 平面
平面![]() ,∴直线
,∴直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
∴![]() .∴
.∴![]() .
.
可取平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
则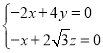 ,取
,取![]() ,则
,则![]() ,
,![]() .∴
.∴![]() ,
,
∴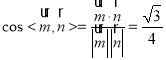 ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】某企业为了解某产品的销售情况,选择某个电商平台对该产品销售情况作调查.统计了一年内的月销售数量(单位:万件),得到该电商平台月销售数量的茎叶图.
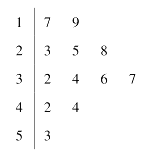
(1)求该电商平台在这一年内月销售该产品数量的中位数和平均数;
(2)该企业与电商签订销售合同时规定:如果电商平台当月的销售件数不低于40万件,当月奖励该电商平台10万元;当月低于40万件没有奖励,用该样本估计总体,从电商平台一个年度内高于该年月销售平均数的月份中任取两个月,求这两个月企业发给电商平台的奖金为20万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设点![]() 分别为曲线
分别为曲线![]() 与曲线
与曲线![]() 上的任意一点,求
上的任意一点,求![]() 的最大值;
的最大值;
(2)设直线![]() (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,四边形
(如图一)的平面展开图(如图二)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的余弦值.
的余弦值.

图一

图二
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图).已知上学所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中x的值;
(2)如果上学所需时间在![]() 的学生可申请在学校住宿,请估计该校800名新生中有多少名学生可以申请住宿.
的学生可申请在学校住宿,请估计该校800名新生中有多少名学生可以申请住宿.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁是一种快捷的交通工具,为我们的出行提供了极大的方便。某高铁换乘站设有编号为①,②,③,④,⑤的五个安全出口,若同时开放其中的两个安全出口,疏散![]() 名乘客所需的时间如下:
名乘客所需的时间如下:
安全出口编号 | ①② | ②③ | ③④ | ④⑤ | ①⑤ |
疏散乘客时间(s) | 120 | 220 | 160 | 140 | 200 |
则疏散乘客最快的一个安全出口的编号是( )
A. ①B. ②C. ④D. ⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,“大衍数列”:0,2,4,8,12….来源于《乾坤谱》中对《易传》“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和.下图是求大衍数列前![]() 项和的程序框图.执行该程序框图,输入
项和的程序框图.执行该程序框图,输入![]() ,则输出的
,则输出的![]() ( )
( )
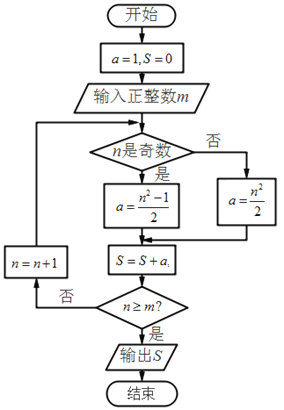
A.100B.140C.190D.250
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com