
【题目】如图,已知圆锥的顶点为S,底面圆O的两条直径分别为![]() 和
和![]() ,且
,且![]() ,若平面
,若平面![]() 平面
平面![]() ,以下四个结论中正确的是( )
,以下四个结论中正确的是( )
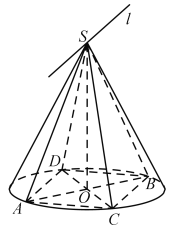
A.![]() 平面
平面![]()
B.![]()
C.若E是底面圆周上的动点,则![]() 的最大面积等于
的最大面积等于![]() 的面积
的面积
D.l与平面![]() 所成的角为45°
所成的角为45°
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某校为了解本校学生网课期间课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.
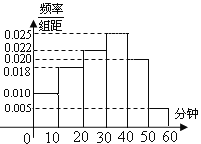
(1)根据频率分布直方图估计抽取样本的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)已知样本中玩电脑游戏时长在![]() 的学生中,男生比女生多1人,现从中任选3人进行回访,求选出的3人中恰有两人是男生的概率.
的学生中,男生比女生多1人,现从中任选3人进行回访,求选出的3人中恰有两人是男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学学生会为了调查爱好游泳运动与性别是否有关,通过随机询问110名性别不同的高中生是否爱好游泳运动得到如下的列联表:
p(k2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由![]() ,并参照附表,得到的正确结论是( )
,并参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“爱好游泳运动与性别有关”
的前提下,认为“爱好游泳运动与性别有关”
B. 在犯错误的概率不超过![]() 的前提下,认为“爱好游泳运动与性别无关”
的前提下,认为“爱好游泳运动与性别无关”
C. 有![]() 的把握认为“爱好游泳运动与性别有关”
的把握认为“爱好游泳运动与性别有关”
D. 有![]() 的把握认为“爱好游泳运动与性别无关”
的把握认为“爱好游泳运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(Ⅰ)写出y与x之间的函数关系式;
(Ⅱ)从第几年开始,该机床开始盈利(盈利额为正值);
(Ⅲ)使用若干年后,对机床的处理方案有两种:
(1)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(2)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“巧值点”,则下列函数中有“巧值点”的是________.
①f(x)=x2;②f(x)=e-x;③f(x)=lnx;④f(x)=tanx;⑤![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.
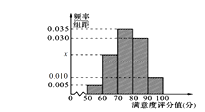
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,判断函数
,判断函数![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)若函数![]() 在
在![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围;
的取值范围;
(3)若存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com