
如图,在底面边长为1,侧棱长为2的正四棱柱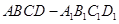 中,P是侧棱
中,P是侧棱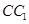 上的一点,
上的一点,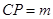 .
.
(1)试确定m,使直线AP与平面BDD1B1所成角为60º;
(2)在线段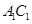 上是否存在一个定点
上是否存在一个定点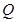 ,使得对任意的m,
,使得对任意的m,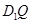 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论. 
(1)60º. (2)Q为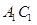 的中点
的中点
解析试题分析:(1)利用空间向量研究线面角,关键在于正确表示各点坐标,正确求出平面一个法向量,正确理解线面角与向量夹角之间互余的关系. 建立空间直角坐标系,则A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0), B1(1,1,1), D1(0,0,2). 所以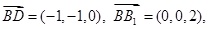
 又由
又由 知
知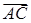 为平面
为平面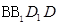 的一个法向量.
的一个法向量. 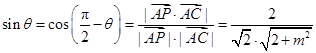 =
= ,解得
,解得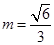 (2)同(1)若在
(2)同(1)若在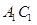 上存在这样的点Q,设此点的横坐标为x,则
上存在这样的点Q,设此点的横坐标为x,则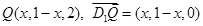 .
.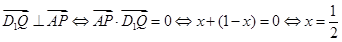 ,即Q为
,即Q为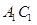 的中点.
的中点.
(1)建立空间直角坐标系,则
A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0),
B1(1,1,1), D1(0,0,2).所以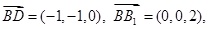
 又由
又由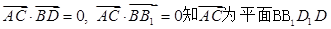 的一个法向量.设
的一个法向量.设 与
与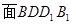 所成的角为
所成的角为 ,
,
则 =
= , 5分
, 5分
解得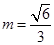 .故当
.故当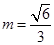 时,直线AP与平面
时,直线AP与平面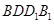 所成角为60º. 7分
所成角为60º. 7分
(2)若在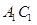 上存在这样的点Q,设此点的横坐标为x,
上存在这样的点Q,设此点的横坐标为x,
则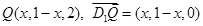 .
.
依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP. 等价于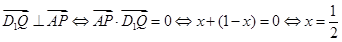
即Q为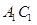 的中点时,满足题设的要求. 14分
的中点时,满足题设的要求. 14分
考点:利用空间向量研究线面关系


科目:高中数学 来源: 题型:解答题
(2013•天津)如图,四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
AA1=AB=2,E为棱AA1的中点.
(1)证明B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的正弦值.
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为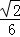 ,求线段AM的长.
,求线段AM的长.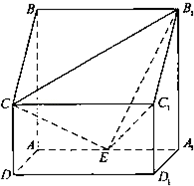
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥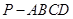 中,
中,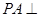 平面
平面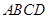 ,底面
,底面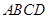 是直角梯形,
是直角梯形,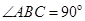 ,
, ∥
∥ ,且
,且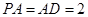 ,
,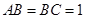 ,
, 为
为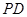 的中点.
的中点.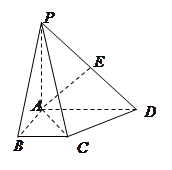
(1)设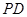 与平面
与平面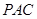 所成的角为
所成的角为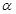 ,二面角
,二面角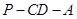 的大小为
的大小为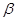 ,求证:
,求证: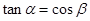 ;
;
(2)在线段 上是否存在一点
上是否存在一点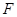 (与
(与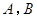 两点不重合),使得
两点不重合),使得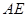 ∥平面
∥平面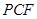 ? 若存在,求
? 若存在,求 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,直三棱柱ABCA1B1C1中,D、E分别是AB、BB1的中点,AA1=AC=CB= AB.
AB.
(1)证明:BC1∥平面A1CD;
(2)求二面角DA1CE的正弦值..
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点A(—3,4),且法向量为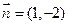 的直线(点法式)方程为
的直线(点法式)方程为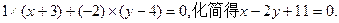 类比以上方法,在空间直角坐标系中,经过点A(1,2,3)且法向量为
类比以上方法,在空间直角坐标系中,经过点A(1,2,3)且法向量为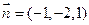 的平面(点法式)方程为 。(请写出化简后的结果)
的平面(点法式)方程为 。(请写出化简后的结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com