练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知命题p，q是简单命题，则“p∨q是真命题”是“￢p是假命题”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分有不必要条件

    分析 由“￢p是假命题”可得：p是真命题，可得“p∨q是真命题”．反之不成立．

    解答 解：由“￢p是假命题”可得：p是真命题，可得“p∨q是真命题”．
    反之不成立，例如p是假命题，q是真命题．
    ∴“p∨q是真命题”是“￢p是假命题”的必要不充分条件．
    故选：B．

    点评 本题考查了复合命题真假的判定方法，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．已知三棱锥O-ABC底面ABC的顶点在半径为$\sqrt{2}$的球O表面上，且AB=$\sqrt{2}$，AC=$\sqrt{2}$，BC=2，则三棱锥O-ABC的体积为（　　）
    A．1B．$\frac{1}{2}$C．$\frac{1}{3}$D．$\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．过点（1，0）且与直线x-$\sqrt{2}$y+3=0平行的直线l被圆（x-6）2+（y-$\sqrt{2}$）2=7所截得的弦长为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

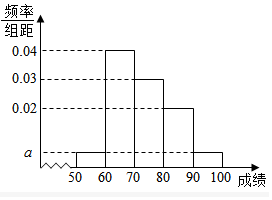    15．某小学1000名学生期中考试数学成绩的频率分布直方图如图所示．其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．根据统计学的知识估计成绩在[80，90）内的人数约为200．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设函数g（x）是R上的偶函数，当x＜0时，g（x）=ln（1-x），函数$f（x）=\left\{\begin{array}{l}{x^3}，x≤0\\ g（x），x＞0\end{array}\right.$满足f（2-x2）＞f（x），则实数x的取值范围是（　　）
    A．（-∞，1）∪（2，+∞）B．（-∞，-2）∪（1，+∞）C．（1，2）D．（-2，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．函数y=-arccos2x的反函数为y=$\frac{1}{2}$cosx，（0，π）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知向量$\overrightarrow a\;，\;\;\overrightarrow b$都是非零向量，“$\overrightarrow a•\overrightarrow b=|{\overrightarrow a}|•|{\overrightarrow b}|$”是“$\overrightarrow a∥\overrightarrow b$”的（　　）
    A．充分非必要条件B．必要非充分条件
    C．充分必要条件D．既非充分也非必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．进位制是人们为了计数和运算方便而约定的记数系统，在日常生活中，我们最熟悉、最常用的是十进制．如图是实现将某进制数a化为十进制数b的程序框图，若输入的k=2，a=110，n=3，则输出的b=（　　）
    A．14B．12C．6D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．下面有五个命题：
    ①终边在y轴上的角的集合是$\{β|β=2kπ+\frac{π}{2}，\;k∈Z\}$；
    ②若扇形的弧长为4cm，面积为4cm2，则这个扇形的圆心角的弧度数是2；
    ③函数y=cos2（$\frac{π}{4}$-x）是奇函数；
    ④函数y=4sin（2x-$\frac{π}{3}$）的一个对称中心是（$\frac{π}{6}$，0）；
    ⑤函数y=tan（-x-π）在$[-π，-\frac{π}{2}）$上是增函数．
    其中正确命题的序号是②③④（把你认为正确命题的序号都填上）．

    查看答案和解析>>

    同步练习册答案